13 Introducción al análisis de diversidad

¿Qué entendemos por diversidad? Al menos podemos conceptualizar diversidad a dos niveles: diversidad genética o morfológica, y biodiversidad. En el estudio de comunidades, tomamos prestado el concepto de biodiversidad de ecología de comunidades donde estamos interesados en la riqueza de especies (número de especies diferentes en una comunidad o diversidad alfa), en las diferencias y similitudes entre comunidades (diversidad beta), y en algunos casos en la diversidad total de un región o paisaje ecológico (landscape; diversidad gama).

En la figura observamos la diversidad de aves en dos regiones, X e Y, y cuatro sitios, 1-4 (figura tomada de Community Ecology de Mittelbach). La diversidad alfa es mayor en los sitios 1 y 3 con 5 especies cada uno. La diversidad beta mide la cantidad de cambio o turnover de especies entre sitios. En la figura, la región Y tiene una diversidad beta mayor que la región X porque el cambio o turnover de especies entre el sitio 2 y el 4 es mayor que entre el sitio 1 y el 3 (que tienen las mismas 5 especies). La diversidad gama mide la diversidad total dentro de una región, por lo tanto en nuestro ejemplo la diversidad gama es mayor en la región Y porque contiene 6 especies en total versus la región X que tiene 5 especies.

13.1 Medidas de riqueza, uniformidad, dominancia, diversidad filogenética (diversidad alfa)

En el contexto metagenómico, medimos diversidad alfa usando una serie de medidas prestadas de ecología que nos permiten caracterizar una comunidad microbiana. phyloseq tiene una función muy útil que nos permite calcular y graficar hasta siete medidas, i .e., Observed (simplemente el número de taxa o riqueza), Chao1 (la riqueza ajustada por probabilidad de no observar especies), ACE (riqueza que toma en cuenta la abundancia relativa), Shannon (abundancia relativa de taxa), Simpson (1 - la probabilidad de que observemos aleatoriamente dos bacterias en una comunidad y que pertenezcan a diferentes especies ), Inverse Simpson ( 1 / Simpson), y Fisher (riqueza tomando en cuenta abundancia).

• En phyloseq simplemente llamamos la función plot_richness y podemos visualizar las medidas de diversidad.

plot_richness(psd5, color = "species", x = "species", measures = c("Observed", "Chao1", "Shannon")) + geom_boxplot(aes(fill = species), alpha=.7) + scale_color_manual(values = c("#a6cee3", "#b2df8a", "#fdbf6f")) + scale_fill_manual(values = c("#a6cee3", "#b2df8a", "#fdbf6f"))

En el ejemplo, solo graficamos Observed, Chao1 y Shannon usando el argumento measures = c("Observed", "Chao1", "Shannon"). Si quisieramos obtener todas las medidas simplemente eliminamos este argumento y por defecto phyloseq graficará todo.

¿Hay un efecto significativo de la diversidad alfa según especie de ballena? Eso lo podríamos probar rápidamente con un análisis de varianza (ANOVA). Para este ejemplo utilicemos otra medida de diversidad, una que phyloseq no incorpora. Faith’s Phylogenetic Diversity es un índice introducido por Daniel Faith en 1992 que no solo considera número de especies sino que también considera qué tanto se parecen estas especies filogenéticamente. Esto es muy relevante porque nos entrega una medida rápida para evaluar prioridades de conservación de ecosistemas, o si se trata de comunidades microbianas, donde tenemos mayor probabilidad de encontrar funciones génicas novedosas.

# Guardamos un dataframe con las medidas de diversidad alfa
alpha_pd <- estimate_pd(psd5)
# Combinamos la metadata con alpha.diversity
data <- cbind(sample_data(psd5), alpha_pd) 
# Y calculamos un ANOVA
psd5.anova <- aov(PD ~ species, data) 
# install.packages("xtable")
library(xtable)
psd5.anova.table <- xtable(psd5.anova)
kable(psd5.anova.table, caption = "Tabla ANOVA", digits = 5, format = "markdown")

Table 13.1: Tabla ANOVA

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
species	2	40.46002	20.23001	5.21047	0.00741
Residuals	82	318.37078	3.88257	NA	NA

• El paquete microbiome ofrece otras herramientas para evaluar diversidad que son accesibles fácilmente a través de su función global.

tab <- global(psd5, index = "all")

head(tab) %>%
  kable(format = "html", col.names = colnames(tab), digits = 2) %>%
  kable_styling() %>%
  kableExtra::scroll_box(width = "100%", height = "300px")

	observed	chao1	diversity_inverse_simpson	diversity_gini_simpson	diversity_shannon	diversity_fisher	diversity_coverage	evenness_camargo	evenness_pielou	evenness_simpson	evenness_evar	evenness_bulla	dominance_dbp	dominance_dmn	dominance_absolute	dominance_relative	dominance_simpson	dominance_core_abundance	dominance_gini	rarity_log_modulo_skewness	rarity_low_abundance	rarity_rare_abundance
SRR6442697	31	49.00	6.95	0.86	2.18	4.10	3	0.76	0.64	0.22	0.10	0.30	0.27	0.40	2099	0.27	0.14	0.26	0.95	2.06	0.01	0.13
SRR6442698	38	41.50	3.67	0.73	1.91	5.78	2	0.29	0.53	0.10	0.14	0.28	0.49	0.62	2015	0.49	0.27	0.67	0.96	2.06	0.02	0.10
SRR6442699	25	37.25	6.46	0.85	2.04	3.12	3	0.57	0.63	0.26	0.07	0.31	0.26	0.41	2461	0.26	0.15	0.47	0.96	2.04	0.00	0.14
SRR6442700	53	63.00	7.71	0.87	2.41	6.10	3	0.18	0.61	0.15	0.08	0.27	0.23	0.42	8300	0.23	0.13	0.61	0.94	2.05	0.01	0.01
SRR6442701	48	68.25	4.52	0.78	2.04	5.95	2	0.28	0.53	0.09	0.10	0.24	0.41	0.54	7742	0.41	0.22	0.23	0.95	2.05	0.01	0.03
SRR6442702	42	82.50	4.87	0.79	1.76	4.35	3	0.12	0.47	0.12	0.07	0.15	0.28	0.49	19137	0.28	0.21	0.46	0.97	2.05	0.01	0.00

La función global nos da 26 medidas de diversidad que nos ayudan a entender la estructura de las comunidades microbianas. En general, estas medidas se dividen en riqueza, diversidad, dominancia, rareza, cobertura y uniformidad.

• El paquete microbiome ofrece funciones para calcular cada uno de estos aspectos de las comunidades microbianas.

# Riqueza
tab <- richness(psd5)
# Dominancia
tab <- dominance(psd5, index = "all")
# Rareza
tab <- rarity(psd5, index = "all")
# Cobertura
tab <- coverage(psd5, threshold = 0.5)
# Desigualdad
tab <- inequality(psd5)
# Uniformidad
tab <- evenness(psd5, "all")

• Veamos un ejemplo concreto estimando diversidad, graficando los resultados y calculando significancia estadística. Para esto usamos el paquete ggpubr que genera “publication-ready plots”, algo que siempre es deseable (ejecuta library(ggpubr)).

# Generamos un objeto `phyloseq` sin taxa que sume 0 reads
psd5.2 <- prune_taxa(taxa_sums(psd5) > 0, psd5)
# Calculamos los índices de diversidad
tab <- diversities(psd5.2, index = "all")
# Y finalmente visualizamos la tabla de resultados
head(tab) %>%
  kable(format = "html", col.names = colnames(tab), digits = 2) %>%
  kable_styling() %>%
  kableExtra::scroll_box(width = "100%", height = "310px")

	observed	chao1	diversity_inverse_simpson	diversity_gini_simpson	diversity_shannon	diversity_fisher	diversity_coverage	evenness_camargo	evenness_pielou	evenness_simpson	evenness_evar	evenness_bulla	dominance_dbp	dominance_dmn	dominance_absolute	dominance_relative	dominance_simpson	dominance_core_abundance	dominance_gini	rarity_log_modulo_skewness	rarity_low_abundance	rarity_rare_abundance
SRR6442697	31	49.00	6.95	0.86	2.18	4.10	3	0.76	0.64	0.22	0.10	0.30	0.27	0.40	2099	0.27	0.14	0.26	0.95	2.06	0.01	0.13
SRR6442698	38	41.50	3.67	0.73	1.91	5.78	2	0.29	0.53	0.10	0.14	0.28	0.49	0.62	2015	0.49	0.27	0.67	0.96	2.06	0.02	0.10
SRR6442699	25	37.25	6.46	0.85	2.04	3.12	3	0.57	0.63	0.26	0.07	0.31	0.26	0.41	2461	0.26	0.15	0.47	0.96	2.04	0.00	0.14
SRR6442700	53	63.00	7.71	0.87	2.41	6.10	3	0.18	0.61	0.15	0.08	0.27	0.23	0.42	8300	0.23	0.13	0.61	0.94	2.05	0.01	0.01
SRR6442701	48	68.25	4.52	0.78	2.04	5.95	2	0.28	0.53	0.09	0.10	0.24	0.41	0.54	7742	0.41	0.22	0.23	0.95	2.05	0.01	0.03
SRR6442702	42	82.50	4.87	0.79	1.76	4.35	3	0.12	0.47	0.12	0.07	0.15	0.28	0.49	19137	0.28	0.21	0.46	0.97	2.05	0.01	0.00

• Ahora necesitamos extraer la metadata de nuestro objeto phyloseq.

psd5.2.meta <- meta(psd5.2)

head(psd5.2.meta) %>%
  kable(format = "html", col.names = colnames(psd5.2.meta), digits = 2) %>%
  kable_styling() %>%
  kableExtra::scroll_box(width = "100%", height = "500px")

	sample_ID	bioproject_accession	study	biosample_accession	experiment	run	SRA_Sample	geo_loc_name	collection_date	sample_type	species	common_name	AvgSpotLen
SRR6442697	EMA4	PRJNA428495	SRP128093	SAMN08292292	SRX3533985	SRR6442697	SRS2809259	Chile: Estrecho_Magallanes	2017	skin	Megaptera novaeangliae	humpback whale	501
SRR6442698	EMA3	PRJNA428495	SRP128093	SAMN08292291	SRX3533984	SRR6442698	SRS2809258	Chile: Estrecho_Magallanes	2017	skin	Megaptera novaeangliae	humpback whale	500
SRR6442699	EMA2	PRJNA428495	SRP128093	SAMN08292284	SRX3533983	SRR6442699	SRS2809257	Chile: Estrecho_Magallanes	2017	skin	Megaptera novaeangliae	humpback whale	501
SRR6442700	EMA19	PRJNA428495	SRP128093	SAMN08292283	SRX3533982	SRR6442700	SRS2809256	Chile: Estrecho_Magallanes	2017	skin	Megaptera novaeangliae	humpback whale	500
SRR6442701	EMA21	PRJNA428495	SRP128093	SAMN08292286	SRX3533981	SRR6442701	SRS2809255	Chile: Estrecho_Magallanes	2017	skin	Megaptera novaeangliae	humpback whale	499
SRR6442702	EMA20	PRJNA428495	SRP128093	SAMN08292285	SRX3533980	SRR6442702	SRS2809254	Chile: Estrecho_Magallanes	2017	skin	Megaptera novaeangliae	humpback whale	500

• Luego agregamos la tabla de diversidad a la metadata.

psd5.2.meta$Shannon <- tab$diversity_shannon
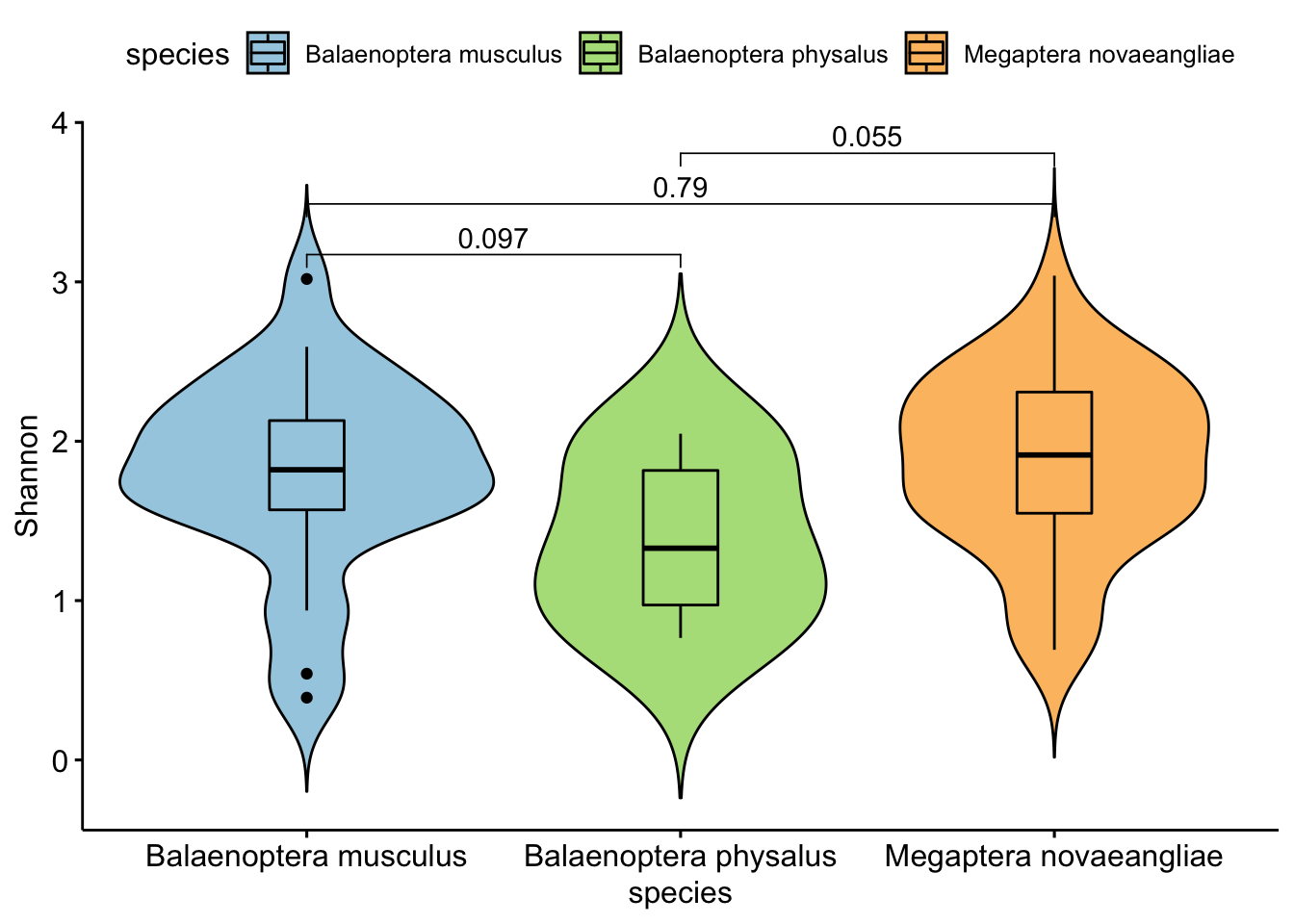
psd5.2.meta$InverseSimpson <- tab$diversity_inverse_simpson

• En este ejercicio nos interesa comparar la diversidad entre especies de ballenas. Recordemos que tenemos datos para tres especies de ballenas: azul, fin y jorobada. Necesitamos crear una lista de comparasiones de a pares para poder visualizar y calcular significancia estadística de manera simultánea.

# Obtenemos las variables desde nuestro objeto `phyloseq`
spps <- levels(psd5.2.meta$species)
# Creamos una lista de lo que queremos comparar
pares.spps <- combn(seq_along(spps), 2, simplify = FALSE, FUN = function(i)spps[i])
# Imprimimos en pantalla el resultado
print(pares.spps)

## [[1]]
## [1] "Balaenoptera musculus" "Balaenoptera physalus"
## 
## [[2]]
## [1] "Balaenoptera musculus"  "Megaptera novaeangliae"
## 
## [[3]]
## [1] "Balaenoptera physalus"  "Megaptera novaeangliae"

• Con la función ggviolin podemos generar un gráfico de violín en un solo paso de la siguiente forma.

p1 <- ggviolin(psd5.2.meta, x = "species", y = "Shannon",
 add = "boxplot", fill = "species", palette = c("#a6cee3", "#b2df8a", "#fdbf6f"))  
print(p1)

• Ahora necesitamos evaluar la significancia estadística entre los estimados de diversidad de las muestras de ballenas. De nuevo, en una línea, tenemos nuestra figura lista para el artículo.

p1 <- p1 + stat_compare_means(comparisons = pares.spps)
print(p1)

13.2 Diversidad beta y escalamiento multidimensional (Bray-Curtis, UniFrac, t-SNE)

En cuanto a diversidad beta podemos calcular similitud global a través de todas las muestras de interés o también podemos cuantificar la divergencia de un grupo y compararla con la divergencia de otro.

• Veamos este último caso primero.

# Calculamos las divergencias para ballena azul y jorobada
div.azul <- divergence(subset_samples(psd5, species == "Balaenoptera musculus"), apply(abundances(subset_samples(psd5, species == "Balaenoptera musculus")), 1, median))
div.joro <- divergence(subset_samples(psd5, species == "Megaptera novaeangliae"), apply(abundances(subset_samples(psd5, species == "Megaptera novaeangliae")), 1, median))
# transformamos el resultado anterior en _dataframes_
data.frame(div.azul) -> df.div.azul
data.frame(div.joro) -> df.div.joro
# Gather
library(tidyverse)
df.div.azul <- gather(df.div.azul, sample, divergence)
df.div.joro <- gather(df.div.joro, sample, divergence)

# Agregamos columnas a nuestros _dataframes_
mutate(df.div.azul, species = "Blue Whale") -> df.div.azul
mutate(df.div.joro, species = "Humpback Whale") -> df.div.joro

# Cambiamos los nombres de las columans de manera que sean iguales an ambos _dataframes_
colnames(df.div.azul) <- c("samples", "divergence", "species")
colnames(df.div.joro) <- c("samples", "divergence", "species")
# Los combinamos en un _dataframe_
rbind(df.div.azul, df.div.joro) -> div.boxplot

# Y finalmente graficamos y realizamos una comparación estadística
p2 <- ggboxplot(data = div.boxplot, x = "species", y = "divergence", fill = "species", palette = c("#a6cee3", "#fdbf6f"))
p2 + stat_compare_means(comparisons = list(c("Blue Whale", "Humpback Whale")))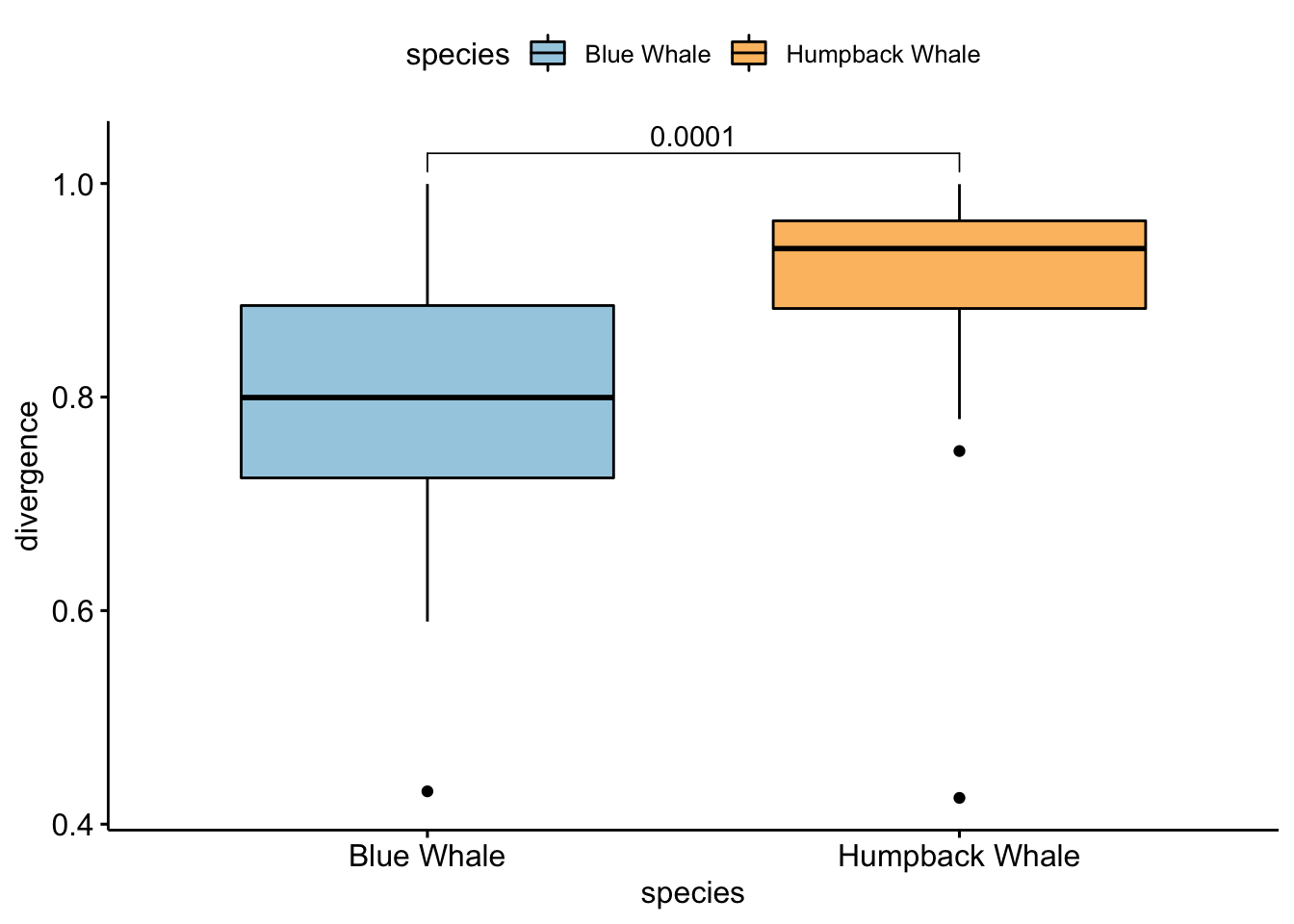

Existen diferentes medidas de similitud (o disimilitud) disponibles que nos permiten entender las relaciones entre nuestras muestras. En general todas producen matrices de distancia comparables. El paquete phyloseq ofrece un gran número de medidas de distancia. Las más populares son UniFrac y Weighted UniFrac (medidas que consideran filogenia) y otras independientes de filogenia como: Jaccard, Manhattan, Euclidian, Bray-Curtis, Canberra, etc. Por otra parte, la matriz de distancia resultante no se usa en aislación sino que en conjunto con algún método de ordinación o escalamiento multidimensional (ordination). De nuevo, phyloseq ofrece un gran número de métodos entre los cuales se encuentran: detrended y canonical correspondence analysis, Double Principle Coordinate Analysis, Non-metric MultiDimenstional Scaling, y MDS/PCoA.

• Probemos entonces hacer un análisis tipo PCoA con una matriz de distancia que considera las relaciones filogenéticas y otra que no.

psd5.mds.unifrac <- ordinate(psd5, method = "MDS", distance = "unifrac")
evals <- psd5.mds.unifrac$values$Eigenvalues
pord1 <- plot_ordination(psd5, psd5.mds.unifrac, color = "geo_loc_name") +
  labs(col = "geo_loc_name") +
  coord_fixed(sqrt(evals[2] / evals[1]))

psd5.mds.bray <- ordinate(psd5, method = "MDS", distance = "bray")
evals <- psd5.mds.bray$values$Eigenvalues
pord2 <- plot_ordination(psd5, psd5.mds.bray, color = "geo_loc_name") +
  labs(col = "geo_loc_name") +
  coord_fixed(sqrt(evals[2] / evals[1]))

grid.arrange(pord1, pord2)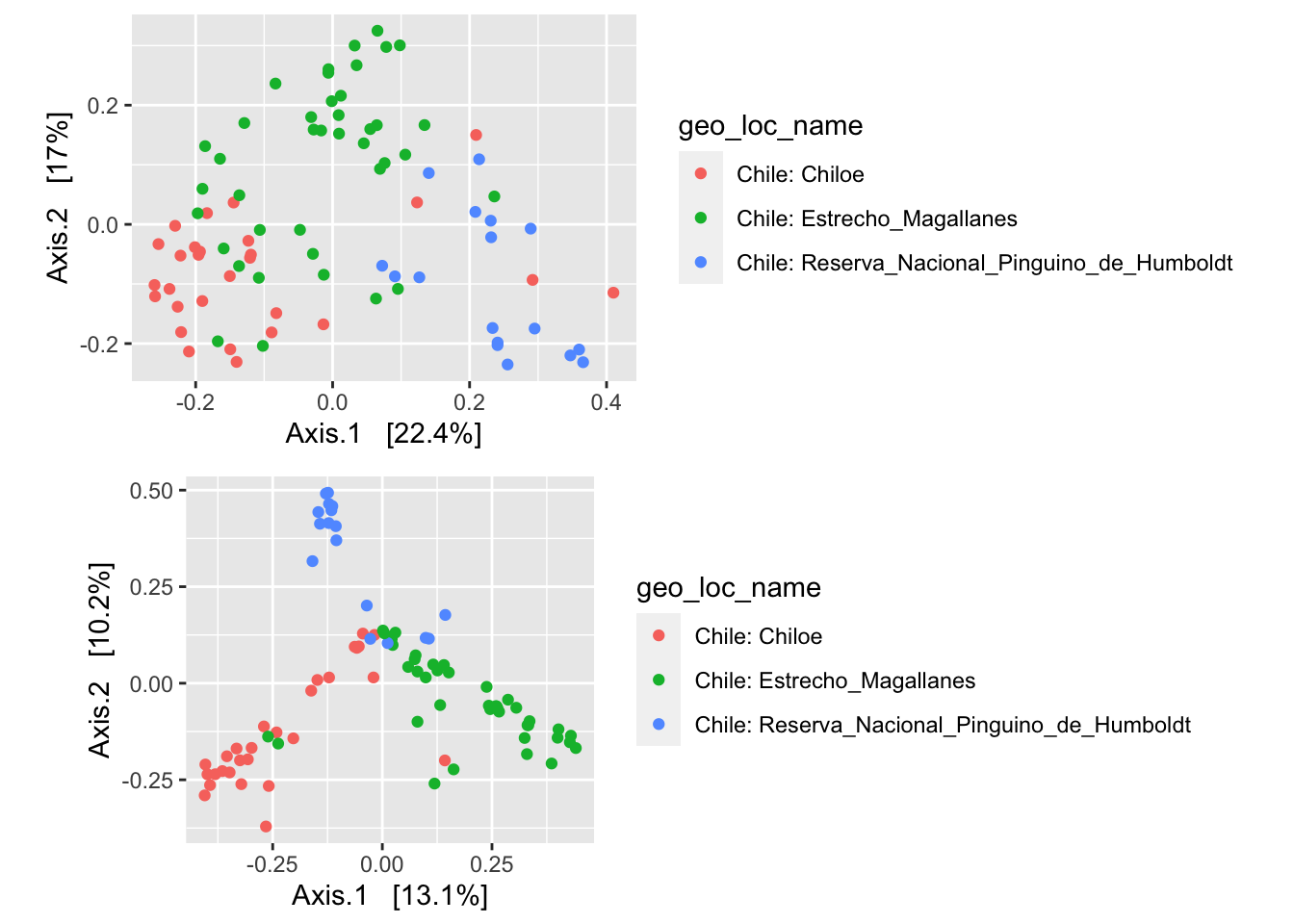

Nota que los gráficos de dispersión donde se visualiza este tipo de análisis están escalados según la cantidad de variación que los ejes explican. En general lo que estos métodos pretenden hacer es tratar de encontrar el menor número de vectores matemáticos que maximicen la separación entre las muestras (puntos en el gráfico). Esto nace de la imposibilidad de graficar eficientemente datos multidimencionales. Los datos que estamos analizando ciertamente son multidimensionales en el sentido que tenemos más de 100 taxa que varían simultáneamente en cada una de las 90+ muestras que tenemos. Volviendo a los ejes, estos no suman 100% porque hay otros ejes que no estamos usando para graficar y que contribuyen con el resto de la variación. Al graficarlos de manera simétrica distorsionaríamos las relaciones entre los puntos, especialmente si estamos comparando dos o más gráficos.

En específico para comunidades microbianas, el método de doble análisis de coordenadas principales o (DPCoA) es muy apropiado porque analiza conjuntamente dos tipos de datos: una tabla de disimilitud que representa diferencias entre especies y una matriz de abundancia que representa la distribución de especies entre las comunidades. El resultado final es un ensamble del espacio multidimensional que correlacionan las especies con las comunidades. El método fue publicado en 2004.

• Veamos un ejemplo con nuestros datos.

psd5.dpcoa.unifrac <- ordinate(psd5, method = "DPCoA", distance = "dpcoa")
evals <- psd5.dpcoa.unifrac$eig
pord3 <- plot_ordination(psd5, psd5.dpcoa.unifrac, color = "species", shape = "geo_loc_name") +
  labs(col = "Species") +
  coord_fixed(sqrt(evals[2] / evals[1])) +
  scale_color_manual(values = c("#a6cee3", "#b2df8a", "#fdbf6f")) + 
  scale_fill_manual(values = c("#a6cee3", "#b2df8a", "#fdbf6f")) +
  geom_point(size=4)
pord3

• Ahora exploremos escalamiento multidimensional usando un método reciente conocido como t-SNE o t-Distributed Stochastic Neighbor Embedding. t-SNE difiere de otros métodos en que hace énfasis en las distancias locales en vez de las distancias globales, de esta forma generando una mayor resolución o separación entre los puntos o muestras.

library(tsnemicrobiota)
tsne_res <- tsne_phyloseq(psd5, distance= "dpcoa", perplexity = 8, verbose=0, rng_seed = 3901)

# Graficamos
pord4 <- plot_tsne_phyloseq(psd5, tsne_res, color = "species", shape = "geo_loc_name") +
  geom_point(size=4) +
  scale_color_manual(values = c("#a6cee3", "#b2df8a", "#fdbf6f")) + 
  scale_fill_manual(values = c("#a6cee3", "#b2df8a", "#fdbf6f"))

grid.arrange(pord3, pord4)

Ambos gráficos usan distintos métodos pero la misma medida de distancia. Los resultados son similares aunque las agrupaciones de puntos o muestras ocupan distinto espacio en el gráfico.

• Otro uso de estas medidas es a través de la visualización de la densidad de las muestras en el espacio.

method <- "tsne"
trans <- "hellinger"
distance <- "euclidean"

# Matriz de distancia
psd5 <- microbiome::transform(psd5, trans)

# Calculamos similitud entre muestras
dm <- vegdist(otu_table(psd5), distance)

# Corremos t-SNE
tsne_out <- Rtsne(dm, dims = 2, perplexity = 8) 
proj <- tsne_out$Y
rownames(proj) <- rownames(otu_table(psd5))
data.frame(proj) -> proj
proj$species <- sample_data(psd5)[,11]

pland <- plot_landscape(proj[,1:2], legend = T, size = 4) 
print(pland)

13.3 Análisis de abundancias y visualizaciones

13.3.1 Gráfico de barras apiladas

Una manera muy eficiente de obtener una visión general de la composición de las muestras es a través de un gráfico de barras apiladas. Existe una variadad de funciones que pueden hacer esto, sin embargo vamos a usar el paquete creado por un ex-miembro del laboratorio ya que tiene la ventaja de poder agrupar por hierarchical clustering las muestras entre otras ventajas.

# Necesitamos obtener las taxa más abundantes, en este caso el top 15
top15 <- get_top_taxa(physeq_obj = psd5, n = 15, relative = T,
                       discard_other = T, other_label = "Other")
# Ya que no todas las taxa fueron clasificadas a nivel de especie, generamos etiquetas compuestas de distintos rangos taxonómicos para el gráfico
top15 <- name_taxa(top15, label = "", species = F, other_label = "Other")
# Finalmente graficamos
fantaxtic_bar(top15, color_by = "Family", label_by = "Genus", facet_by = NULL, grid_by = NULL, other_color = "Grey") -> ptop15

##                          Level N.color.shades Central.color
## 1           Cardiobacteriaceae              1       #6495ED
## 2            Flavobacteriaceae              1       #EDBC64
## 3                Moraxellaceae              5       #9A64ED
## 4  Gammaproteobacteria (Class)              2       #B7ED64
## 5             Xanthomonadaceae              1       #ED64DA
## 6           Enterobacteriaceae              2       #64ED77
## 7             Pseudomonadaceae              2       #ED6473
## 8             Burkholderiaceae              1       #64EDDE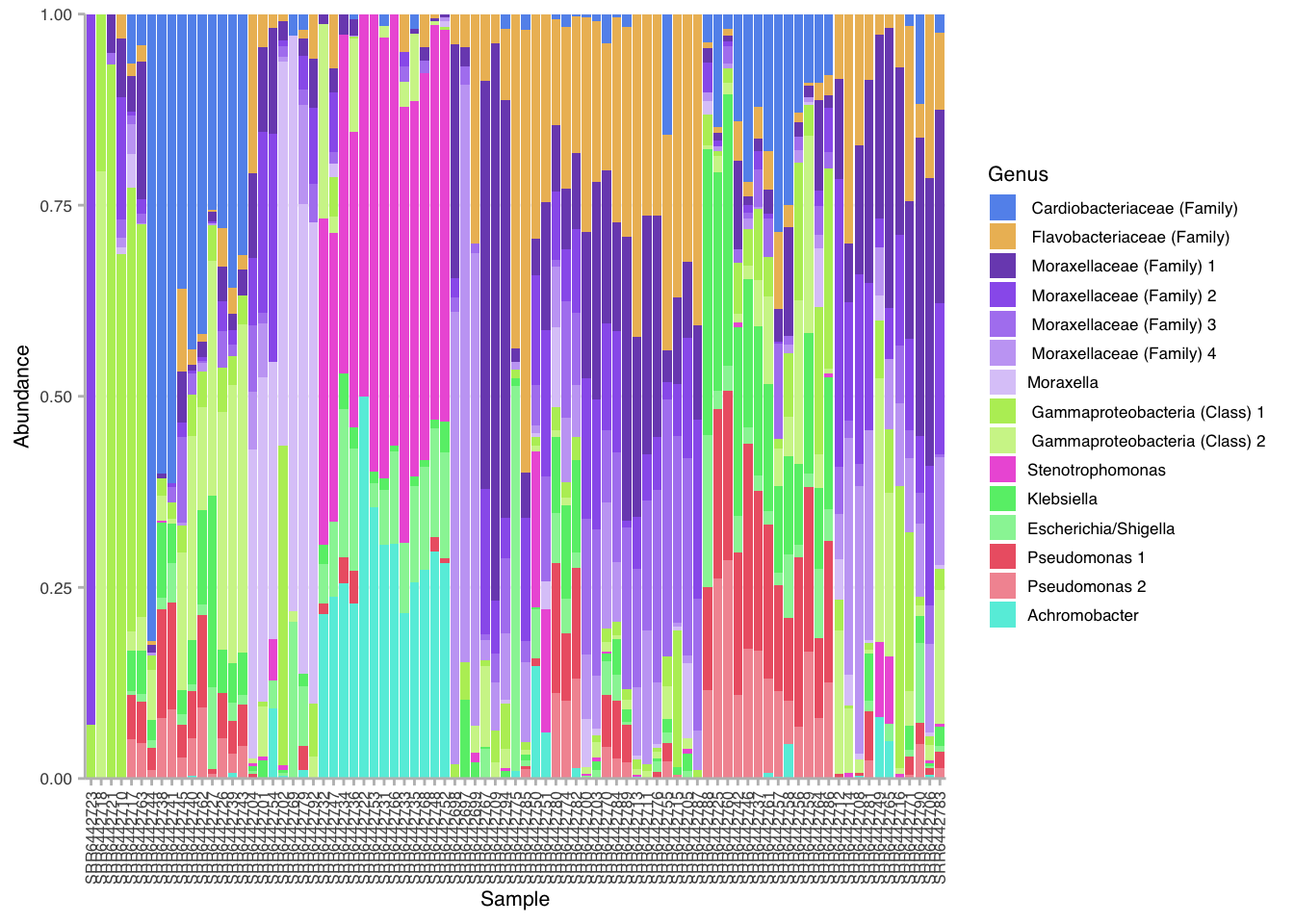

ptop15

Podemos ver que existen patrones relativamente claros en el gráfico solamente a partir de los colores. Aunque tenemos el nombre de las muestras bajo cada barra, sería mejor poder parcelar este gráfico de manera que quede claro qué muestras corresponden a qué especie de ballena.

• La función fantaxtic_bar ofrece estas posibilidades a través de los argumentos facet_by y grid_by. Grafiquemos de nuevo.

fantaxtic_bar(top15, color_by = "Family", label_by = "Genus", facet_by = "species", grid_by = NULL, other_color = "Grey") -> ptop15.2

##                          Level N.color.shades Central.color
## 1           Cardiobacteriaceae              1       #6495ED
## 2            Flavobacteriaceae              1       #EDBC64
## 3                Moraxellaceae              5       #9A64ED
## 4  Gammaproteobacteria (Class)              2       #B7ED64
## 5             Xanthomonadaceae              1       #ED64DA
## 6           Enterobacteriaceae              2       #64ED77
## 7             Pseudomonadaceae              2       #ED6473
## 8             Burkholderiaceae              1       #64EDDE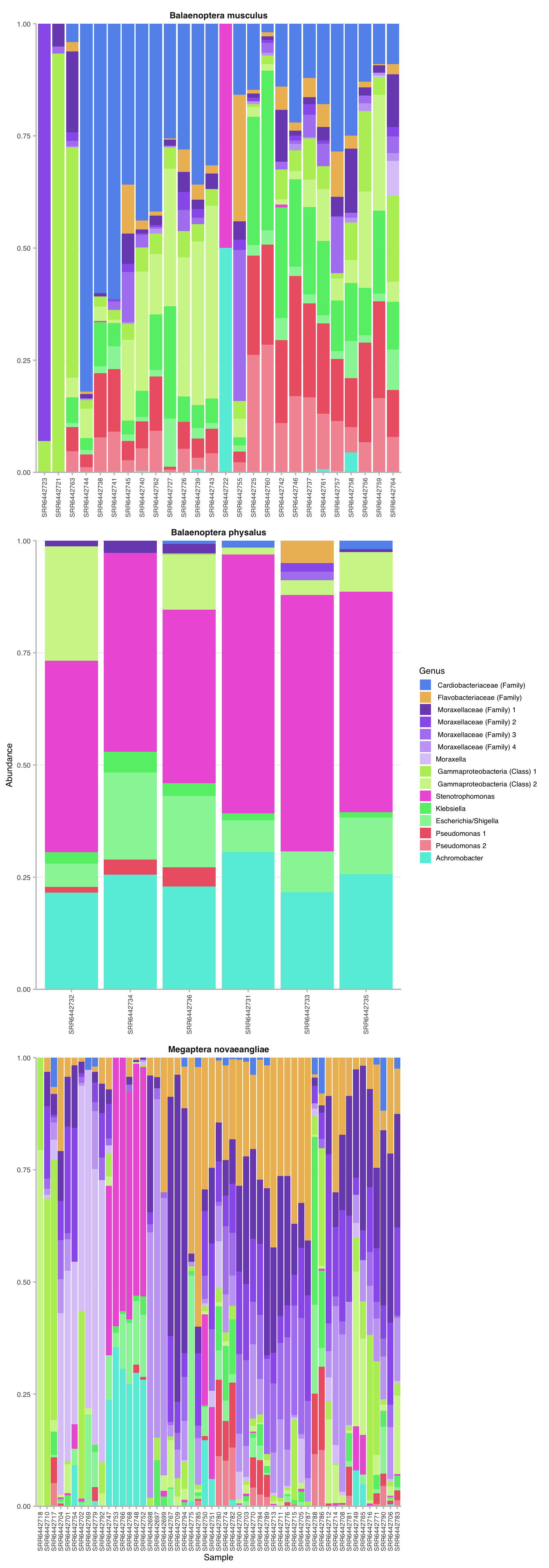

ptop15.2

Ahora queda más claro y se puede observar que las distintas especies de ballena tienen un patrón similar entre sí que es diferente entre las otras, con algunas excepciones. Por ejemplo, para ballena jorobada podemos ver un conjunto de muestras que no se parecen al resto. Usando las herramientas ya aprendidas, ¿A qué corresponden esas muestras?

13.3.2 Diferentes visualizaciones de abundancias

Veamos ahora otras herramientas que nos permiten examinar la composición de estas comunidades microbianas. El paquete ampvis2, desarrollado por Mads Albertsen y Kasper Skytte Andersen, nos permite hacer precisamente esto. Primero transformemos el objeto phyloseq con el cual hemos estado trabajando en un objeto ampvis2.

library(ampvis2)
# Necesitamos extraer la tabla de read counts y la tabla de taxonomía del objeto psd5
# Generamos una copia para no sobreescribir psd5
obj <- psd5
# Cambiamos la orientación de la otu_table
t(otu_table(obj)) -> otu_table(obj)
# Extraemos las tablas
otutable <- data.frame(OTU = rownames(phyloseq::otu_table(obj)@.Data),
                       phyloseq::otu_table(obj)@.Data,
                       phyloseq::tax_table(obj)@.Data,
                       check.names = FALSE
)
# Extraemos la metadada
metadata <- data.frame(phyloseq::sample_data(obj), 
                       check.names = FALSE
)
# ampvis2 requiere que 1) los rangos taxonómicos sean siete y vayan de Kingdom a Species y 2) la primera columna de la metadata sea el identificador de cada muestra
# Entonces duplicamos la columna Género y le cambiamos el nombre a Especie
otutable$Species = otutable$Genus
# Reordenamos la metadata
metadata <- metadata[,c("run","sample_ID","bioproject_accession","study","biosample_accession","experiment","SRA_Sample","geo_loc_name","collection_date","sample_type","species","common_name","AvgSpotLen")]

# finalmente generamos el objeto ampvis
av2 <- amp_load(otutable, metadata)

• Ahora echemos un vistazo a la estructura de las comunidades utilizando “rank abundance curves”.

amp_rankabundance(av2, log10_x = T, group_by = "species")

El gráfico nos muestra que en la medida que vamos sumando las taxa de mayor a menor abundancia (Rank Abundance) la abundancia de reads cumulativa va aumentando. Lo importante de observar es la forma de la curva. Una curva que sube rápidamente nos indica que las comunidades están dominadas por unas cuantas taxa. En cambio, lo que observamos en nuestros datos es que las taxa más abundantes solamente dan cuenta de aproximadamente el 25% de la abundancia cumulativa de reads.

• Veamos ahora qué taxa corresponde a ese 25%. Para esto podemos usar la función amp_heatmap.

amp_heatmap(av2, 
            group_by = "species", 
            facet_by = "geo_loc_name", 
            plot_values = TRUE,
            tax_show = 20,
            tax_aggregate = "Genus",
            tax_add = "Phylum",
            plot_colorscale = "sqrt",
            plot_legendbreaks = c(1, 5, 10)
            )

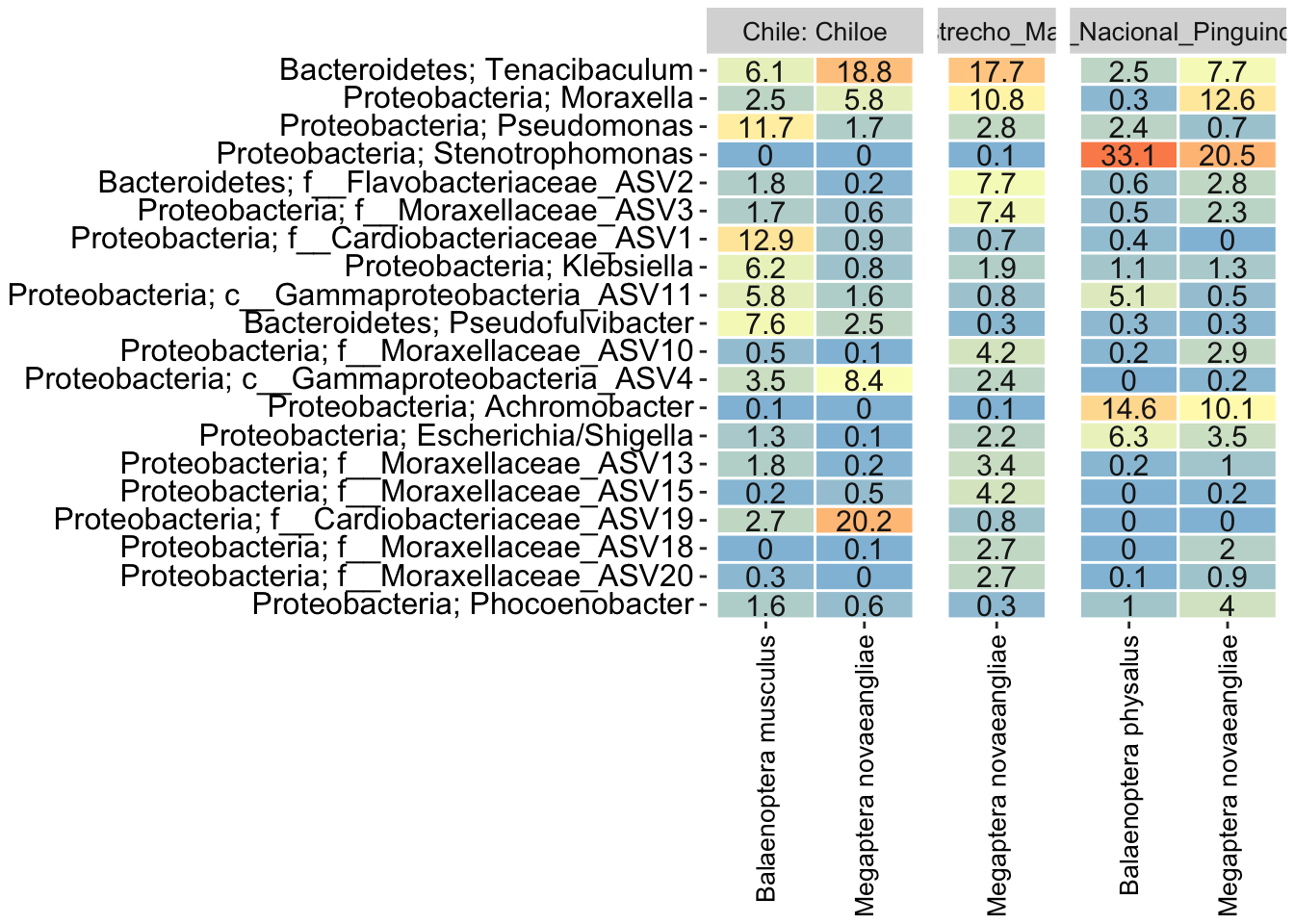
Tenacibaculum parece ser el género más abundante para todas las muestras en todas los sitios de muestreo con excepción de Balaenoptera physalus que está dominada por Stenotrphomonas. Moraxella y distintas variantes de Cardiobacteriaceae de género no conocido. Justamente estos resultados se ajustan a lo conocido para cetáceos y otros mamíferos marinos.

• También podemos realizar una visualización similar pero usando Box Plots.

amp_boxplot(av2,
            group_by = "species",
            tax_show = 20,
            tax_aggregate = "Genus",
            tax_add = "Phylum",
            adjust_zero = T,
            plot_log = T) +
  scale_color_manual(values = c("#a6cee3", "#b2df8a", "#fdbf6f")) + 
  scale_fill_manual(values = c("#a6cee3", "#b2df8a", "#fdbf6f"))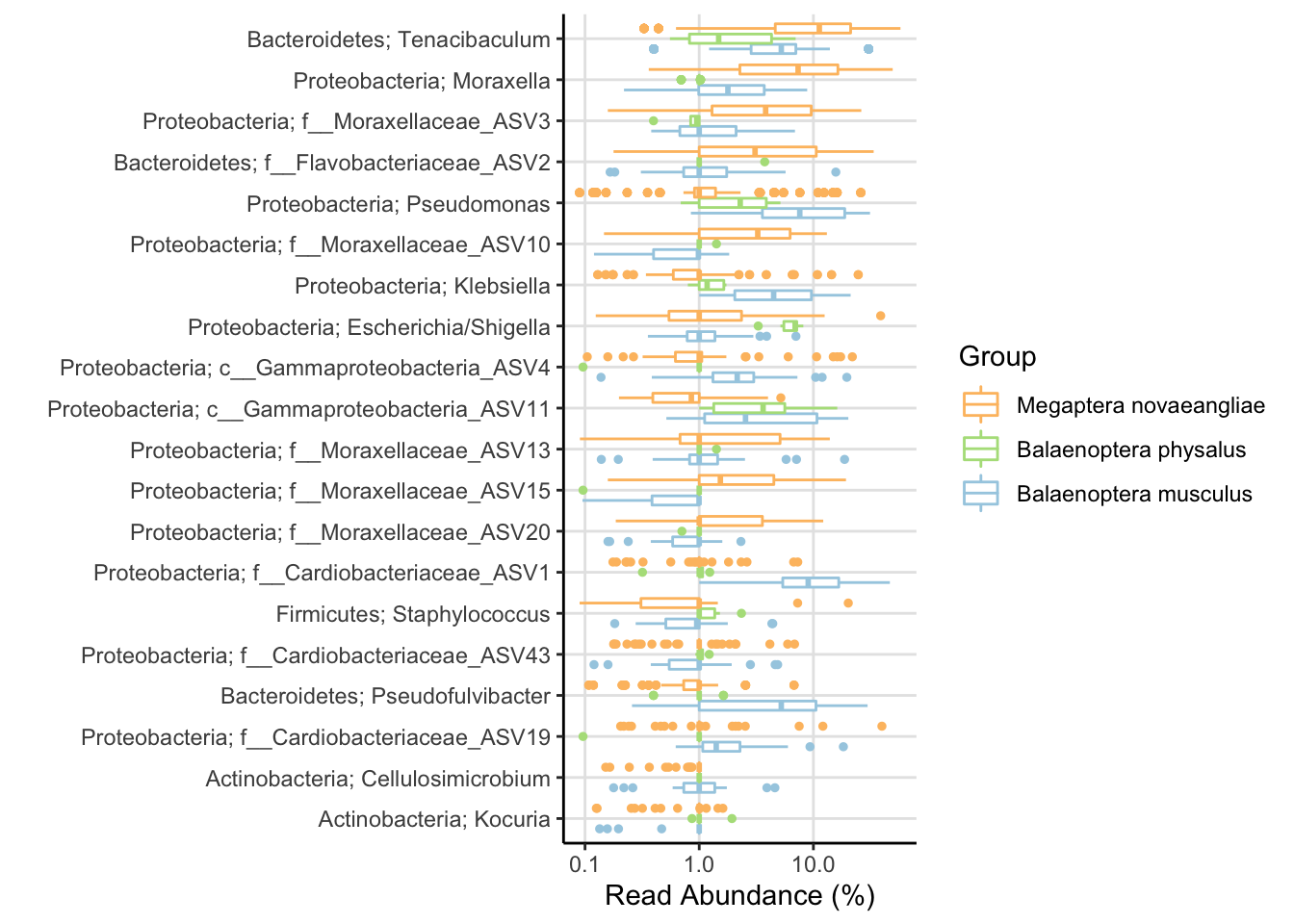

• Veamos ahora si es que algunos de estos microorganismos están compartidos entre todas las muestras. Para esto debemos calcular el core microbiome o el conjunto de taxa compartidas entre un cierto umbral porcentual de muestras y de prevalencia intra-muestra.

amp_core(av2,
         group_by = "species")

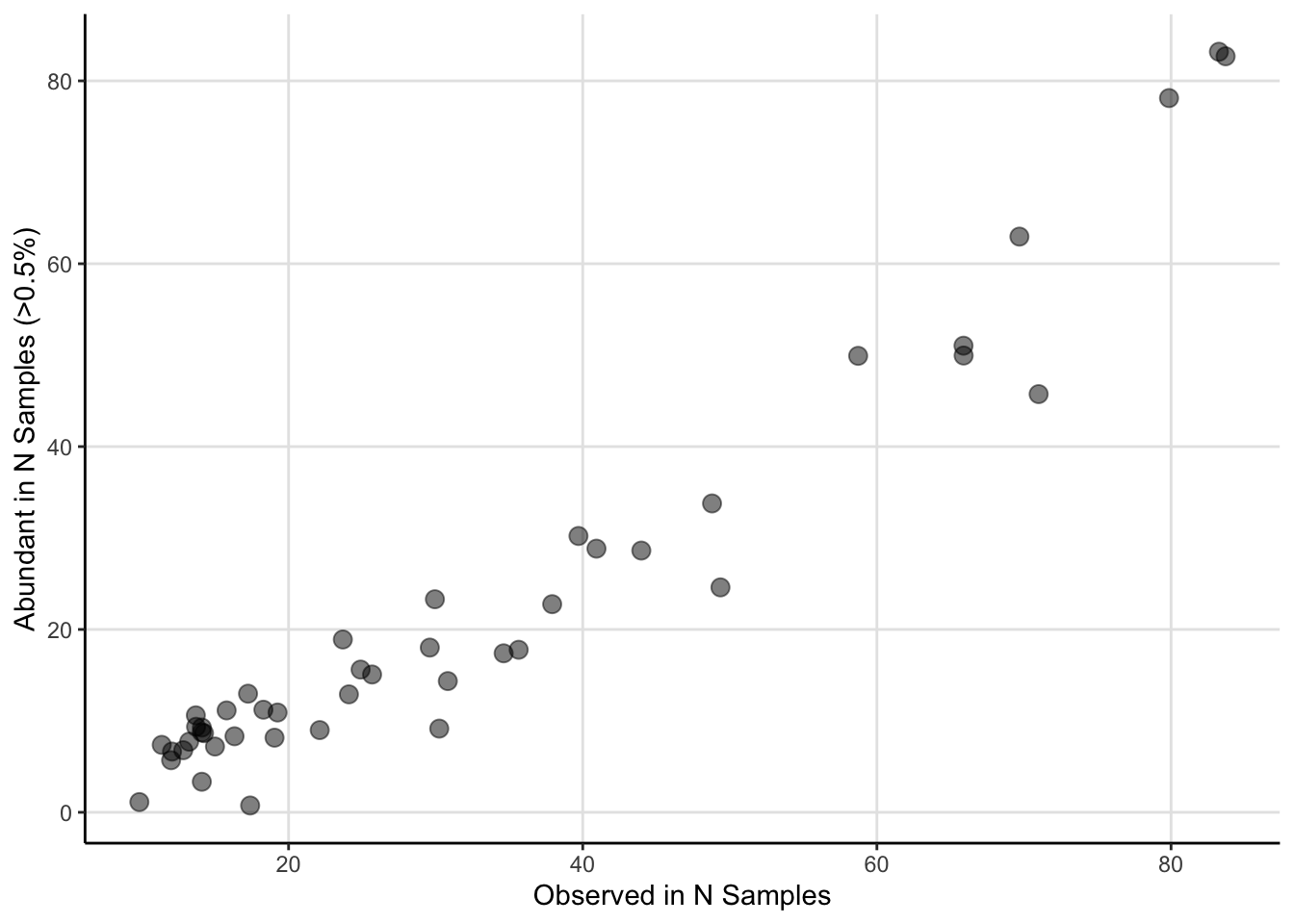
• Y visto de otra manera en un diagrama de Venn.

amp_venn(av2, group_by = "species", cut_a = 0, cut_f = 50, text_size = 3)

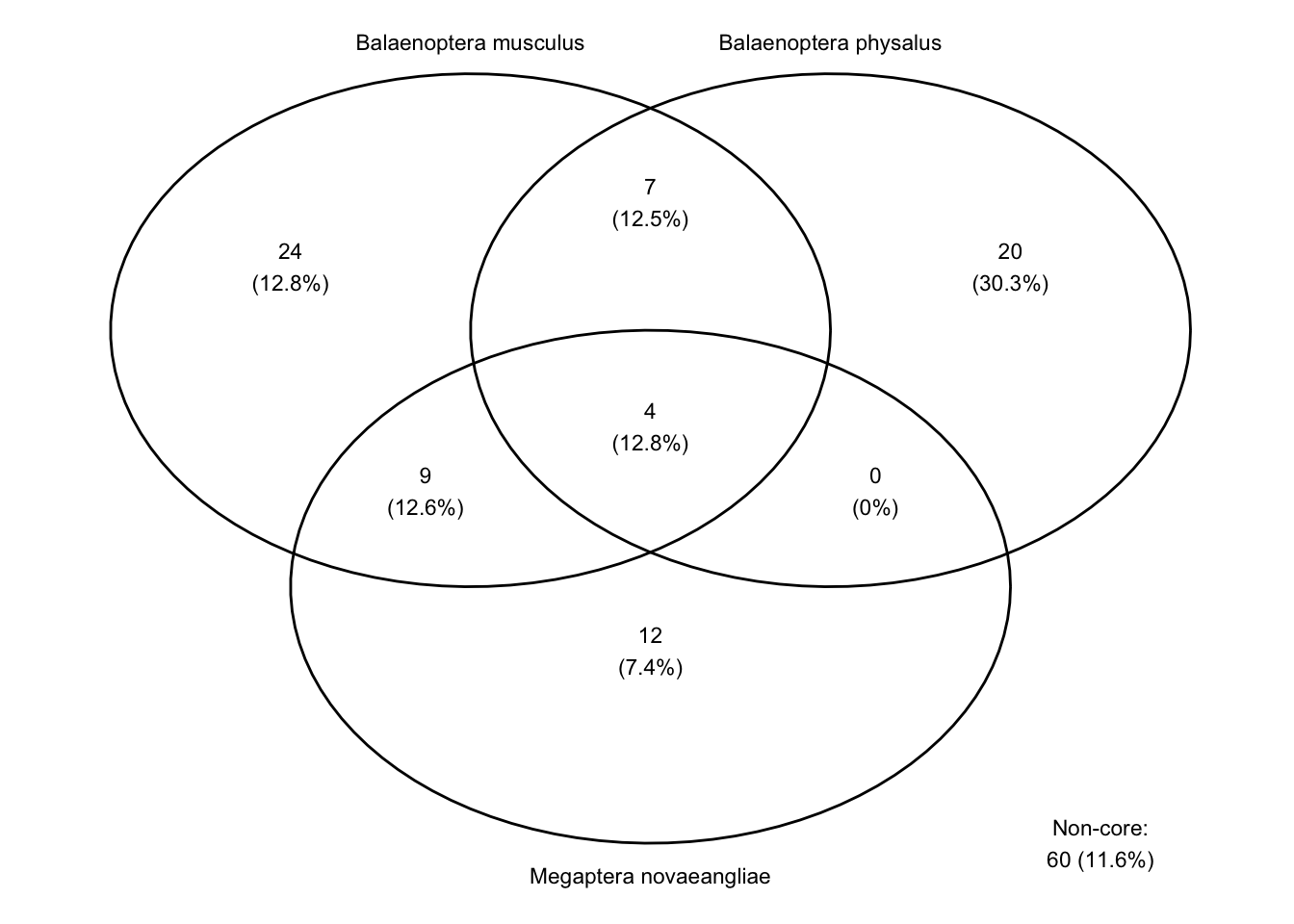
13.3.3 Análisis de abundancia diferencial de microorganismos

Hasta ahora hemos visto principalmente análisis exploratorios y algunos test estadísticos para diversidad alfa y beta. Sin embargo, muchas veces queremos determinar exactamente qué taxa está más representada en una condición versus otra y en qué medida. El procedimiento es análogo al análisis de expresión diferencial de genes en transcritómica, e.g., RNA-seq. Es tan así que justamente ocupamos uno de los paquetes de R más populares en transcriptómica, DESeq2. Ahora, nuestras muestras se secuenciaron al mismo tiempo y se intentó que se produjera una profundidad uniforme a través de todas las muestras. En la práctica esto no ocurre y al momento de analizar las muestras en el contexto del análisis diferencial de abundancia debemos corregir por dos situaciones: el tamaño desigual de las muestras (en número de reads) y la correlación de la variabilidad de los datos con la media de éstos. Para esto último, utilizamos una transformación llamada Variance Stabilizing Transformation, cuyo objetivo es encontrar una función ƒ que se aplique a los valores de read counts, de tal forma que en los nuevos valores y = ƒ(x), la variabilidad de y no se relacione con sus valores medios.

• Comencemos por aplicar la transformación en los datos.

# Creamos un objeto DESeq2 con la función `phyloseq_to_deseq2`
diagdds = phyloseq_to_deseq2(psd4, ~species)
# Calculamos los factores de tamaño como parte de la normalización de las muestras
# calculate geometric means prior to estimate size factors
gm_mean = function(x, na.rm=TRUE){
    exp(sum(log(x[x > 0]), na.rm=na.rm) / length(x))
}
geoMeans = apply(counts(diagdds), 1, gm_mean)
diagdds = estimateSizeFactors(diagdds, geoMeans = geoMeans)

# Normalizamos y realizamos el test paramétrico de Wald para determinar taxa diferencialmente abundante.
diagdds = DESeq(diagdds, test="Wald", fitType="local")

Hasta ahora hemos transformado nuestro objeto phyloseq en un objeto DESeq2 de nombre diagdds, y hemos normalizado las cuentas y realizado un test paramétrico (Wald Test).

• Nos queda entonces revisar los resultados usando la función results.

# Guardamos los resultados en el objeto res
res = results(diagdds, cooksCutoff = FALSE)
# hacemos un poco de aseo y ordenamos la tabla de resultados según p-value, y dejamos los valores NA al final
res = res[order(res$padj, na.last=NA), ]

• Ahora nosotros queremos averiguar sobre ciertos contrastes específicos entre condiciones, e.g., ballena jorobada versus ballena azul. En el contraste, pasamos un vector con el nombre de la columna en la metadata (“species”) e indicamos el numerador de la comparación (“Megaptera novaeangliae”) y el denominador (“Balaenoptera musculus”). Por lo tanto el log2FoldChange positivo indicará que ese microorganismo es más abundante en ballena jorobada que en ballena azul, y viceversa.

res.joro.azul <- results(diagdds, contrast=c("species","Megaptera novaeangliae","Balaenoptera musculus"))

# Veamos qué hay en res.joro.azul
res.joro.azul %>%
  kable(format = "html", col.names = colnames(res.joro.azul)) %>%
  kable_styling() %>%
  kableExtra::scroll_box(width = "100%", height = "400px")  

	baseMean	log2FoldChange	lfcSE	stat	pvalue	padj
ASV1	2719.4817399	-7.1224534	1.0359380	-6.8753665	0.0000000	0.0000000
ASV2	2022.5405509	5.4006313	0.7461453	7.2380427	0.0000000	0.0000000
ASV3	2100.9914000	5.3802668	0.6766070	7.9518346	0.0000000	0.0000000
ASV4	489.6362991	0.8724453	0.8271381	1.0547760	0.2915278	0.3442805
ASV5	1138.1509390	13.0147565	1.3019415	9.9964222	0.0000000	0.0000000
ASV6	45.6810800	5.5840818	1.8653474	2.9935880	0.0027572	0.0049735
ASV7	245.1490808	4.4924803	0.9791466	4.5881589	0.0000045	0.0000168
ASV8	1211.9442253	-3.2250402	0.9315225	-3.4621172	0.0005359	0.0012307
ASV9	148.8626474	4.0117257	0.8333867	4.8137625	NA	NA
ASV10	548.7130326	6.4054200	0.7366579	8.6952434	0.0000000	0.0000000
ASV11	1009.5925018	-5.0854806	0.8255799	-6.1598889	0.0000000	0.0000000
ASV12	658.7876904	-3.2447714	1.0411077	-3.1166530	0.0018292	0.0034895
ASV13	410.6582559	3.0099935	0.8716746	3.4531160	0.0005542	0.0012494
ASV14	140.0717828	3.8198888	1.0080979	3.7892044	NA	NA
ASV15	379.3194323	7.5644546	0.8161418	9.2685548	0.0000000	0.0000000
ASV16	285.7620345	7.6440491	0.9097626	8.4022455	0.0000000	0.0000000
ASV17	379.4487960	14.2183560	1.4003173	10.1536672	0.0000000	0.0000000
ASV18	203.0595008	9.1750665	1.1303913	8.1167175	0.0000000	0.0000000
ASV19	69.8158128	-2.2614994	0.9908843	-2.2823041	0.0224714	0.0331721
ASV20	299.9612618	5.6657701	0.9446883	5.9975021	0.0000000	0.0000000
ASV21	91.1653741	7.8577937	1.1458691	6.8574966	0.0000000	0.0000000
ASV22	522.4807634	-3.8585579	1.1993634	-3.2171718	0.0012946	0.0027209
ASV23	100.3448777	10.0985821	1.3550063	7.4527934	0.0000000	0.0000000
ASV24	345.5275036	8.1857232	1.3845014	5.9123979	0.0000000	0.0000000
ASV25	278.9908685	-2.5125876	1.5875681	-1.5826644	0.1134980	0.1436097
ASV26	62.1557348	-0.4907744	1.4756983	-0.3325709	0.7394582	0.7904553
ASV27	189.6100970	-3.6035868	1.2050796	-2.9903310	0.0027868	0.0049735
ASV28	218.1259662	-0.4960691	0.8838224	-0.5612769	0.5746088	0.6361740
ASV29	348.5666726	-9.2693864	1.2067447	-7.6813154	0.0000000	0.0000000
ASV30	19.9949713	-6.9404408	2.0012541	-3.4680458	NA	NA
ASV31	9.4574754	4.4204992	1.8265012	2.4202006	0.0155119	0.0234571
ASV32	135.9042193	4.6452237	1.0957355	4.2393659	0.0000224	0.0000678
ASV33	12.2150782	3.8067681	1.2271358	3.1021570	NA	NA
ASV34	14.5758192	6.9563749	0.9863495	7.0526474	0.0000000	0.0000000
ASV35	78.7642402	1.0289747	0.8831016	1.1651827	NA	NA
ASV36	15.6844519	4.4745682	1.5457245	2.8948031	0.0037940	0.0065340
ASV37	104.0931206	6.3198854	1.0890983	5.8028606	0.0000000	0.0000000
ASV38	63.0999441	7.0198666	1.2124308	5.7899111	0.0000000	0.0000000
ASV39	71.6857366	-4.1210982	0.9699437	-4.2488015	0.0000215	0.0000666
ASV40	11.7563573	4.6362327	1.8491255	2.5072570	NA	NA
ASV41	63.6924912	6.7765578	1.5717381	4.3115057	0.0000162	0.0000522
ASV42	39.8228286	3.9641573	1.1704109	3.3869791	0.0007067	0.0015108
ASV43	29.6927766	0.6482185	0.9863497	0.6571893	0.5110592	0.5761031
ASV44	4.6851145	-4.9032274	1.1881480	-4.1267818	0.0000368	0.0001061
ASV45	31.3542359	-5.8903163	1.0674036	-5.5183589	0.0000000	0.0000001
ASV46	52.3468950	8.1940044	1.2045392	6.8026052	0.0000000	0.0000000
ASV47	24.3460080	5.1994788	1.1498081	4.5220406	0.0000061	0.0000223
ASV48	9.5531988	-3.1476568	1.9364467	-1.6254807	NA	NA
ASV49	28.1689872	4.3313913	1.3563693	3.1933718	0.0014062	0.0028817
ASV50	89.6234760	-8.8288920	1.2859692	-6.8655549	0.0000000	0.0000000
ASV51	42.8236021	7.0692754	1.5947984	4.4327079	0.0000093	0.0000328
ASV52	1.0011767	2.5999491	1.5148878	1.7162651	0.0861135	0.1112300
ASV53	33.2080947	1.4605265	0.9766925	1.4953800	0.1348153	0.1655158
ASV54	82.8130820	-2.1815886	1.1338739	-1.9240134	0.0543529	0.0732583
ASV55	9.1745027	3.2672435	1.9477963	1.6774051	0.0934633	0.1194789
ASV56	11.3403634	4.6971790	1.4994164	3.1326715	0.0017322	0.0034095
ASV57	16.5241450	1.8610673	1.5605106	1.1926015	0.2330255	0.2778381
ASV58	13.2662521	2.8954770	1.4432286	2.0062497	0.0448296	0.0624592
ASV59	99.5242996	-10.6308795	1.2924338	-8.2254731	0.0000000	0.0000000
ASV60	68.5859180	1.1857152	1.2128028	0.9776653	0.3282399	0.3839788
ASV61	2.5896101	0.5237964	0.9994077	0.5241068	NA	NA
ASV62	7.2983417	4.2913582	1.4469920	2.9657096	0.0030199	0.0052741
ASV63	10.6361249	7.2294633	1.8091772	3.9959952	0.0000644	0.0001816
ASV64	83.5838226	-2.6340549	1.2610396	-2.0887963	0.0367261	0.0517504
ASV65	47.6516393	10.1206302	1.4127059	7.1640036	0.0000000	0.0000000
ASV66	70.2942412	5.2089523	1.4217267	3.6638212	0.0002485	0.0006032
ASV67	24.7841554	5.1537365	1.2188111	4.2284950	0.0000235	0.0000695
ASV68	14.2934620	5.5087333	1.4218510	3.8743394	0.0001069	0.0002821
ASV69	21.2132029	1.7036268	1.1444604	1.4885853	0.1365966	0.1660586
ASV70	68.7558900	-0.3460662	1.6848409	-0.2053999	0.8372597	0.8516169
ASV71	6.2303015	-0.2601080	1.2445510	-0.2089974	NA	NA
ASV72	14.6638119	7.0648004	1.6396906	4.3086180	0.0000164	0.0000522
ASV73	7.5897409	5.3428616	1.4510121	3.6821619	0.0002313	0.0005735
ASV74	5.0789582	-1.3853182	1.1394033	-1.2158278	NA	NA
ASV75	19.8697343	24.2907265	1.8316754	13.2614802	0.0000000	0.0000000
ASV76	1.2239068	-1.9354764	1.2311449	-1.5720947	0.1159286	0.1437514
ASV77	9.0374513	-9.8994430	1.4981683	-6.6076975	0.0000000	0.0000000
ASV78	21.1929292	8.8483467	1.6584029	5.3354626	0.0000001	0.0000004
ASV79	13.7751655	-2.6546117	1.4029815	-1.8921217	0.0584748	0.0771369
ASV80	28.3678395	23.0655138	1.6147380	14.2843691	0.0000000	0.0000000
ASV81	9.9644103	-2.8946247	0.7983325	-3.6258383	NA	NA
ASV82	5.5165903	5.0158379	1.8121294	2.7679247	0.0056414	0.0095827
ASV83	22.0290096	7.8115706	1.2982118	6.0171773	0.0000000	0.0000000
ASV84	5.3880867	3.5536543	1.1892872	2.9880540	0.0028076	0.0049735
ASV85	1.7369590	-3.9773770	1.3253471	-3.0010078	0.0026909	0.0049735
ASV86	8.6940194	0.9909398	1.7309680	0.5724772	0.5669987	0.6334040
ASV87	2.6463367	-4.9527209	1.2607597	-3.9283623	0.0000855	0.0002305
ASV88	22.4846884	-7.9573124	1.0142627	-7.8454155	0.0000000	0.0000000
ASV89	29.2974383	-5.7553117	1.0928471	-5.2663465	0.0000001	0.0000005
ASV90	5.5849388	4.5854927	2.0669960	2.2184332	0.0265253	0.0386957
ASV91	16.5698452	-7.4960519	1.3749392	-5.4519154	0.0000000	0.0000002
ASV92	22.6522435	-4.9676859	1.2977662	-3.8278742	0.0001293	0.0003339
ASV93	6.4062042	-4.0851822	1.5797024	-2.5860455	0.0097084	0.0156343
ASV94	1.7970262	3.0983231	1.2328023	2.5132359	0.0119629	0.0190180
ASV95	11.9501380	-7.6996523	1.3118837	-5.8691576	0.0000000	0.0000000
ASV96	2.8351525	0.3828029	1.6800387	0.2278536	0.8197600	0.8470854
ASV97	3.7248506	5.1135350	1.5097237	3.3870667	0.0007064	0.0015108
ASV98	4.3233609	4.8042120	1.9622148	2.4483619	0.0143507	0.0219690
ASV99	2.8243846	3.5024621	1.0975926	3.1910403	0.0014176	0.0028817
ASV100	9.9778511	-4.6282742	1.2648220	-3.6592297	0.0002530	0.0006032
ASV101	7.1881927	-0.4163206	1.6084949	-0.2588262	0.7957694	0.8292050
ASV102	8.2413114	-3.7473291	1.1989296	-3.1255621	0.0017747	0.0034384
ASV103	8.3102765	-6.7562778	1.5258751	-4.4278053	0.0000095	0.0000328
ASV104	6.7857308	5.7064612	1.6741681	3.4085353	0.0006531	0.0014462
ASV105	5.0488641	4.1346140	1.5935323	2.5946219	0.0094695	0.0154502
ASV106	0.9541234	-1.1028164	2.0346151	-0.5420270	0.5877999	0.6450193
ASV107	4.1007567	4.9980913	1.1373183	4.3946286	0.0000111	0.0000372
ASV108	5.4038096	-3.6271094	1.2133551	-2.9893224	0.0027960	0.0049735
ASV109	1.3501927	-0.4206071	1.4415801	-0.2917681	0.7704639	0.8096400
ASV110	2.7371281	3.3005287	1.7374702	1.8996174	0.0574833	0.0766445
ASV111	2.4259080	4.5000589	1.8203672	2.4720611	0.0134337	0.0210857
ASV112	1.5325388	-0.6703858	1.9366425	-0.3461588	0.7292234	0.7862930
ASV113	5.1286581	5.5651234	1.5523269	3.5850202	0.0003371	0.0007886
ASV114	3.2084055	4.2076848	1.5538169	2.7079669	0.0067697	0.0113438
ASV115	1.8693006	4.1459636	1.5967342	2.5965270	0.0094171	0.0154502
ASV116	7.7258899	-6.1720272	1.5544558	-3.9705388	0.0000717	0.0001976
ASV117	4.6721853	-6.3099610	1.6600099	-3.8011586	0.0001440	0.0003645
ASV118	0.9186556	-1.6434260	1.7179194	-0.9566375	0.3387503	0.3925704
ASV119	7.0228498	-1.8945403	0.8629677	-2.1953780	0.0281365	0.0401026
ASV120	0.8432035	0.1593532	1.9188207	0.0830475	0.9338138	0.9338138
ASV121	3.3482616	-2.7839431	1.2669338	-2.1973864	0.0279929	0.0401026
ASV122	3.6359471	-4.5928491	1.8643476	-2.4635155	0.0137582	0.0213252
ASV123	1.7902754	-1.4023022	1.5327540	-0.9148906	0.3602491	0.4136193
ASV124	2.6697932	2.1839877	1.3857261	1.5760602	0.1150119	0.1437514
ASV125	1.1415391	-0.7290996	1.8509376	-0.3939082	0.6936488	0.7544952
ASV126	2.9465902	-1.8431157	1.2640321	-1.4581241	0.1448064	0.1743300
ASV127	2.9109028	0.9547596	1.1013290	0.8669159	0.3859881	0.4391057
ASV128	2.9624475	-4.1618781	1.3116973	-3.1728951	0.0015093	0.0030185
ASV129	2.1092384	-0.3088813	1.5096505	-0.2046045	0.8378811	0.8516169
ASV130	1.4749075	-0.2884521	0.9376518	-0.3076324	0.7583621	0.8037342
ASV131	2.3920165	-2.4765750	1.3681047	-1.8102232	0.0702612	0.0917093
ASV132	1.3600064	0.1650124	1.5324853	0.1076763	0.9142524	0.9216854
ASV133	0.7154383	2.8063290	1.4139574	1.9847338	0.0471741	0.0649954
ASV134	1.0638791	-1.5182223	1.3665996	-1.1109489	NA	NA
ASV135	1.4368076	-4.0800926	1.6943303	-2.4080857	0.0160364	0.0239580
ASV136	0.6620716	-2.3480281	1.2061752	-1.9466725	0.0515740	0.0702767

¿Qué significa cada columna? Revisa la viñeta de DESeq2 aquí.

• Ahora establezcamos un umbral de significancia estadística para los valores de p-value ajustado o padj. Cualquier resultado bajo este umbral será considerado no significativo y viceversa.

# Este es nuestro umbral
alpha = 0.01
# Ordenamos la tabla de resultados
res.joro.azul = res.joro.azul[order(res.joro.azul$padj, na.last=NA), ]
# Filtramos según nuestro umbral alpha
sigtab = res.joro.azul[(res.joro.azul$padj < alpha), ]
# Le agregamos la taxonomía a la tabla
sigtab = cbind(as(sigtab, "data.frame"), as(tax_table(psd5)[rownames(sigtab), ], "matrix"))

# Manipulaciones varias para finalmente graficar los resultados
sigtabgen = subset(sigtab, !is.na(Genus))
# Phylum order
x = tapply(sigtabgen$log2FoldChange, sigtabgen$Phylum, function(x) max(x))
x = sort(x, TRUE)
sigtabgen$Phylum = factor(as.character(sigtabgen$Phylum), levels=names(x))
# Genus order
x = tapply(sigtabgen$log2FoldChange, sigtabgen$Genus, function(x) max(x))
x = sort(x, TRUE)
sigtabgen$Genus = factor(as.character(sigtabgen$Genus), levels=names(x))
ggplot(sigtabgen, aes(y=Genus, x=log2FoldChange, color=Phylum)) + 
    geom_vline(xintercept = 0.0, color = "gray", size = 0.5) +
    geom_point(size=4) + 
    theme(axis.text.x = element_text(angle = -90, hjust = 0, vjust=0.5, size = 10), axis.text.y = element_text(size = 13), legend.text = element_text(size = 13) )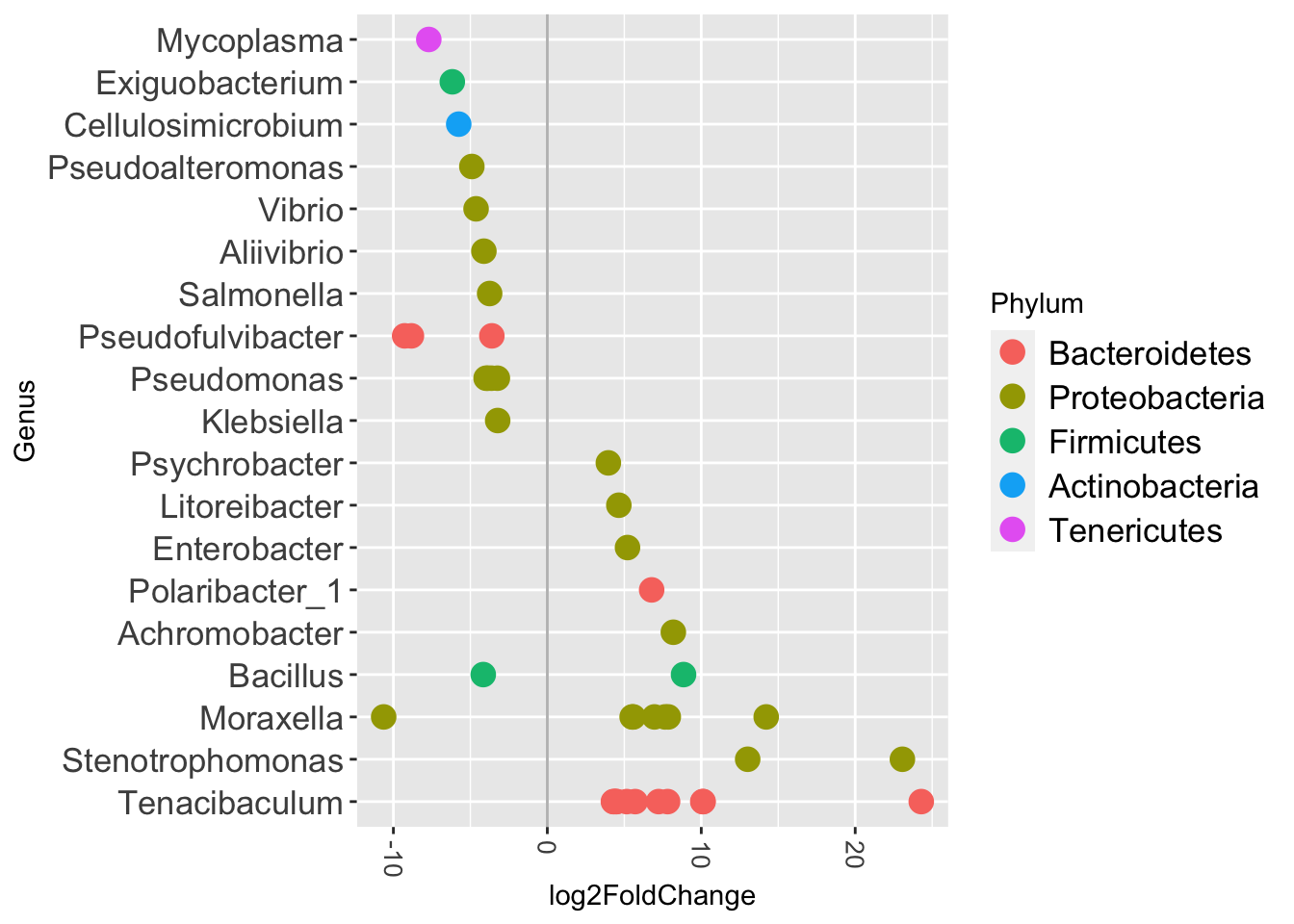

13.3.4 Redes de co-ocurrencia

Para finalizar, vamos a echar un vistazo a las capacidades de phyloseq para generar redes de co-occurrencia. Las redes de co-ocurrencia nos dan pistas sobre potenciales interacciones ecológicas entre organismos. Estas interacciones pueden ser directas o indirectas (no lo podemos determinar a partir de una red) y nos permiten comenzar a descifrar mecanismos ecológicos detrás de la composición de una comunidad microbiana. En general en ecología tenemos distintos tipos de interacciones:

Donde destacan depredación, competición o depredación mutua, y mutualismo. Cada una de estas relaciones podría ser detectada en una red de co-ocurrencia según patrones de correlación positivos o negativos.

• Veamos como generaríamos una red en phyloseq.

plot_net(psd5, type = "taxa", point_label = "Genus", point_size = 10, point_alpha = 0.5, maxdist = 0.5, color = "Phylum", distance = "bray", laymeth = "auto") 

La red generada con phyloseq no es una red de co-ocurrencia propiamente tal. Es más bien una red que representa relaciones de distancia entre taxa o muestras. En nuestro ejemplo usamos muestras. Para una red de co-ocurrencia propiamente tal necesitamos usar las funciones del paquete SpiecEasi.

• Veamos un ejemplo de cómo hacerlo.

library(devtools)
# install_github("zdk123/SpiecEasi")
library(SpiecEasi)
se.mb.psd4 <- spiec.easi(psd4, method='mb', lambda.min.ratio=1e-2,
                           nlambda=20, icov.select.params=list(rep.num=50))
ig2.mb <- adj2igraph(getRefit(se.mb.psd4),  vertex.attr=list(name=taxa_names(psd4)))
plot_network(ig2.mb, psd4, type='taxa', color="Phylum")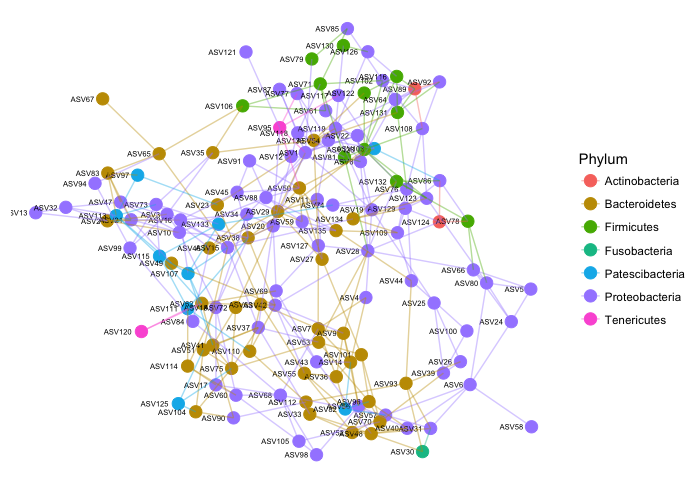

Un tutorial mucho más completo lo pueden encontrar aquí y aquí.