7 Clustering
Clustering se refiere al proceso de agrupar un set de datos de manera que aquellos datos dentro de un mismo cluster o grupo sean más similares entre sí que con datos en otros clusters.
El libro Modern Statistics for Modern Biology (MSMB) presenta muy bien este tema. Revisemos el capítulo 5. Acá, tenemos que revisar los puntos 5.3 y el ejercicio 5.3.1. El resto de nuestra sección de clustering corresponde al ejemplo trabajado del capítulo 5 del MSMB.
- Comenzamos descargando los paquetes necesarios de Bioconductor.
#BiocManager::install(c("flowCore", "flowViz", "flowPeaks", "ggcyto", "labeling", "dbscan", "Hiiragi2013"))
library("flowCore")
library("flowViz")
library("flowPeaks")
library("ggcyto")
library("labeling")
library("dbscan")
fcsB = read.FCS("data/Bendall_2011.fcs")
slotNames(fcsB)## [1] "exprs" "parameters" "description"Mira la estructura del objeto fcsB (usa la función colnames). Cuántas variables fueron medidas?
7.1 Preprocesamiento de datos
- Primero, cargamos la tabla de datos que reporta el mapeo entre isótopos y anticuerpos (markers), y reemplazamos los nombres de los isótopos en las columnas de
fcsBcon lo nombres de los anticuerpos.
## Parsed with column specification:
## cols(
## isotope = col_character(),
## marker = col_character()
## )mt = match(markersB$isotope, colnames(fcsB))
stopifnot(!any(is.na(mt)))
colnames(fcsB)[mt] = markersB$markerAhora generamos el gráfico que muestra el clustering en dos dimensiones.

Otro ejemplo. En el primer gráfico se ve un histograma de la variable CD3all, las células se agrupan alrededor del valor 0 con unas pocos valores más altos. El segundo gráfico es después de la transformación (asinh), los grupos de células caen en dos grupos o tipos.
asinhtrsf = arcsinhTransform(a = 0.1, b = 1)
fcsBT = transform(fcsB,
transformList(colnames(fcsB)[-c(1, 2, 41)], asinhtrsf))
densityplot( ~`CD3all`, fcsB)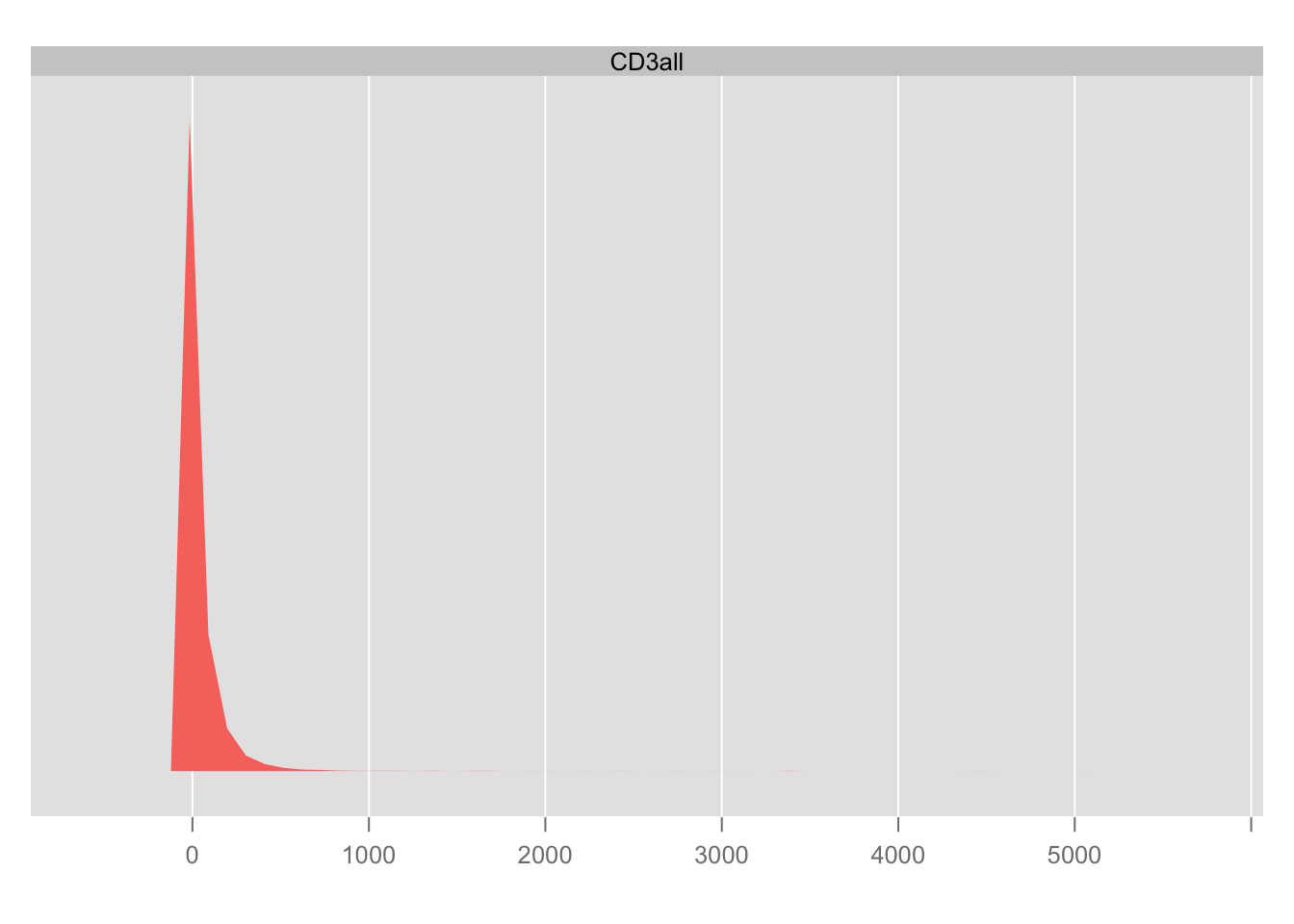
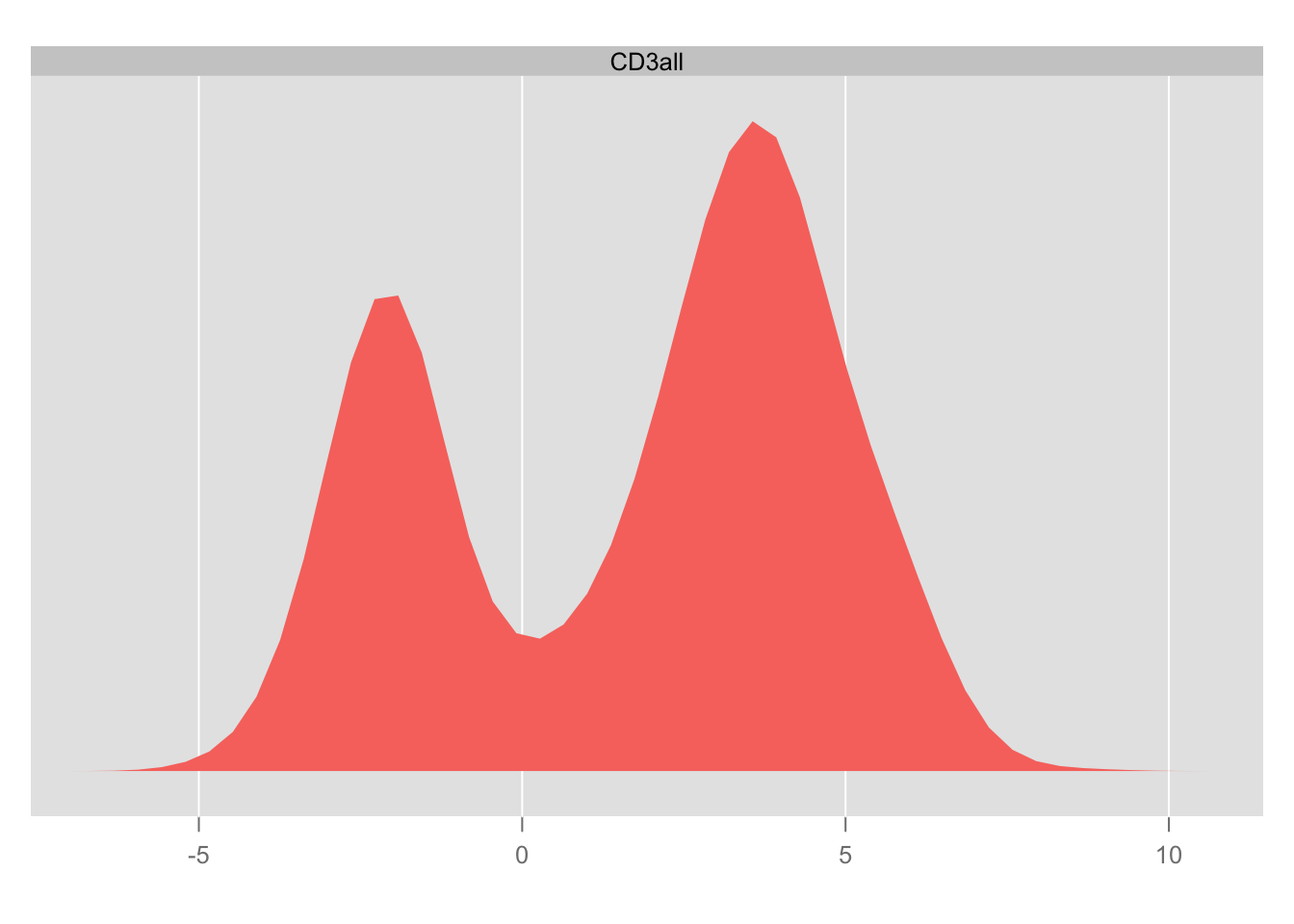
¿Cuántas dimensionas usa el siguiente código para dividir los datos en 2 grupos usando k-means?
kf = kmeansFilter("CD3all" = c("Pop1","Pop2"), filterId="myKmFilter")
fres = flowCore::filter(fcsBT, kf)
summary(fres)## Pop1: 33429 of 91392 events (36.58%)
## Pop2: 57963 of 91392 events (63.42%)fcsBT1 = flowCore::split(fcsBT, fres, population = "Pop1")
fcsBT2 = flowCore::split(fcsBT, fres, population = "Pop2")Proyección de los datos en dos dimensiones.
flowPlot(fcsBT, plotParameters = c("CD3all", "CD56"), logy = FALSE)
contour(fcsBT[, c(40, 19)], add = TRUE)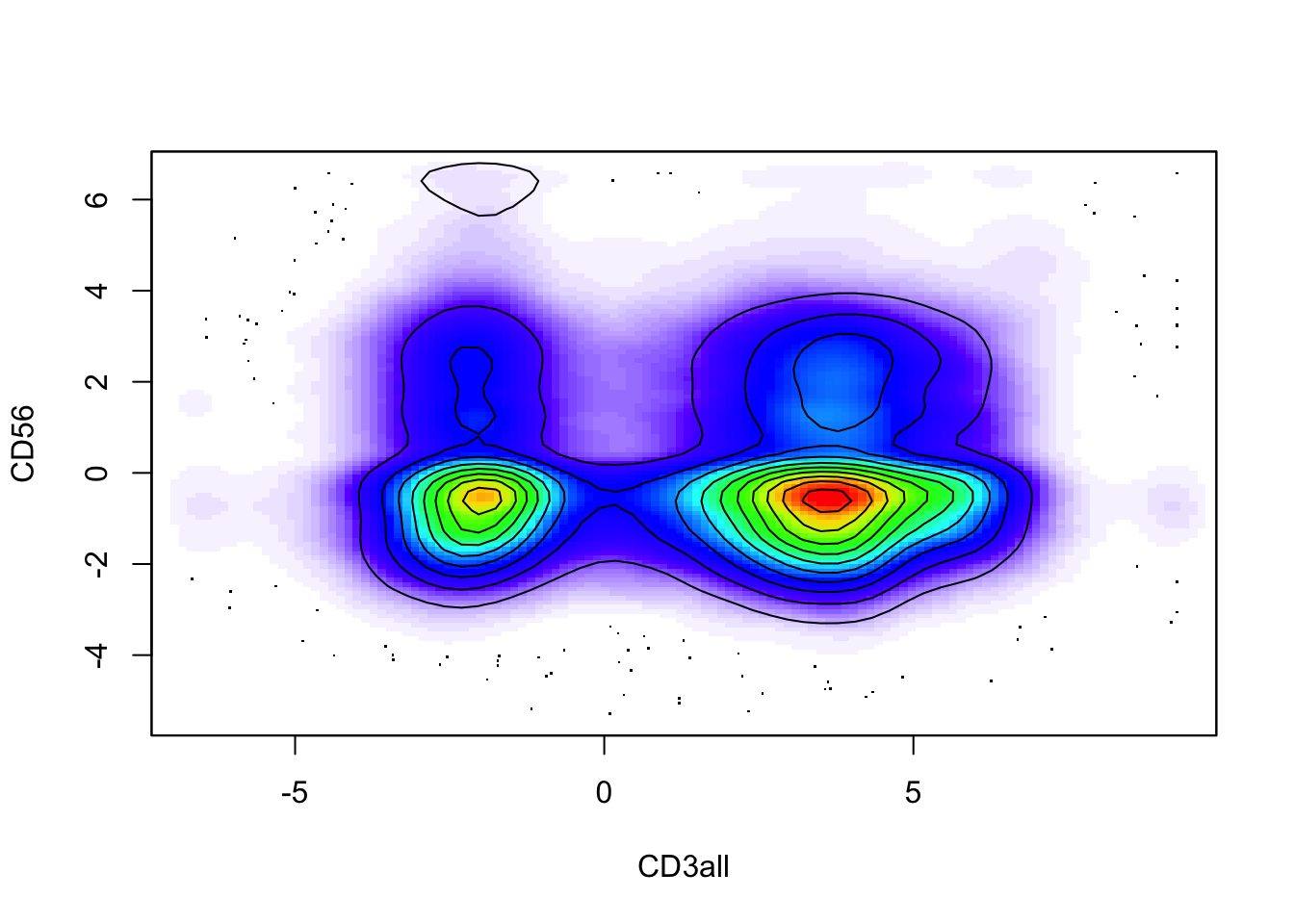
7.2 Clustering basado en densidad
Set de datos como citometría de flujo, que contiene solo algunos anticuerpos (markers) y un largo número de células, son adecuados para density-based clustering. Éste método busca regiones de alta densidad separadas por regiones de baja densidad. Una implementación del método se conoce como dbscan.
mc5 = Biobase::exprs(fcsBT)[, c(15,16,19,40,33)]
res5 = dbscan::dbscan(mc5, eps = 0.65, minPts = 30)
mc5df = data.frame(mc5, cluster = as.factor(res5$cluster))
table(mc5df$cluster)##
## 0 1 2 3 4 5 6 7
## 77655 230 5114 4616 3310 207 231 29## Warning: stat_contour(): Zero contours were generated## Warning in min(x): no non-missing arguments to min; returning Inf## Warning in max(x): no non-missing arguments to max; returning -Inf## Warning: stat_contour(): Zero contours were generated## Warning in min(x): no non-missing arguments to min; returning Inf## Warning in max(x): no non-missing arguments to max; returning -Inf## Warning: stat_contour(): Zero contours were generated## Warning in min(x): no non-missing arguments to min; returning Inf## Warning in max(x): no non-missing arguments to max; returning -Inf## Warning: stat_contour(): Zero contours were generated## Warning in min(x): no non-missing arguments to min; returning Inf## Warning in max(x): no non-missing arguments to max; returning -Inf
## Warning: stat_contour(): Zero contours were generated## Warning in min(x): no non-missing arguments to min; returning Inf## Warning in max(x): no non-missing arguments to max; returning -Inf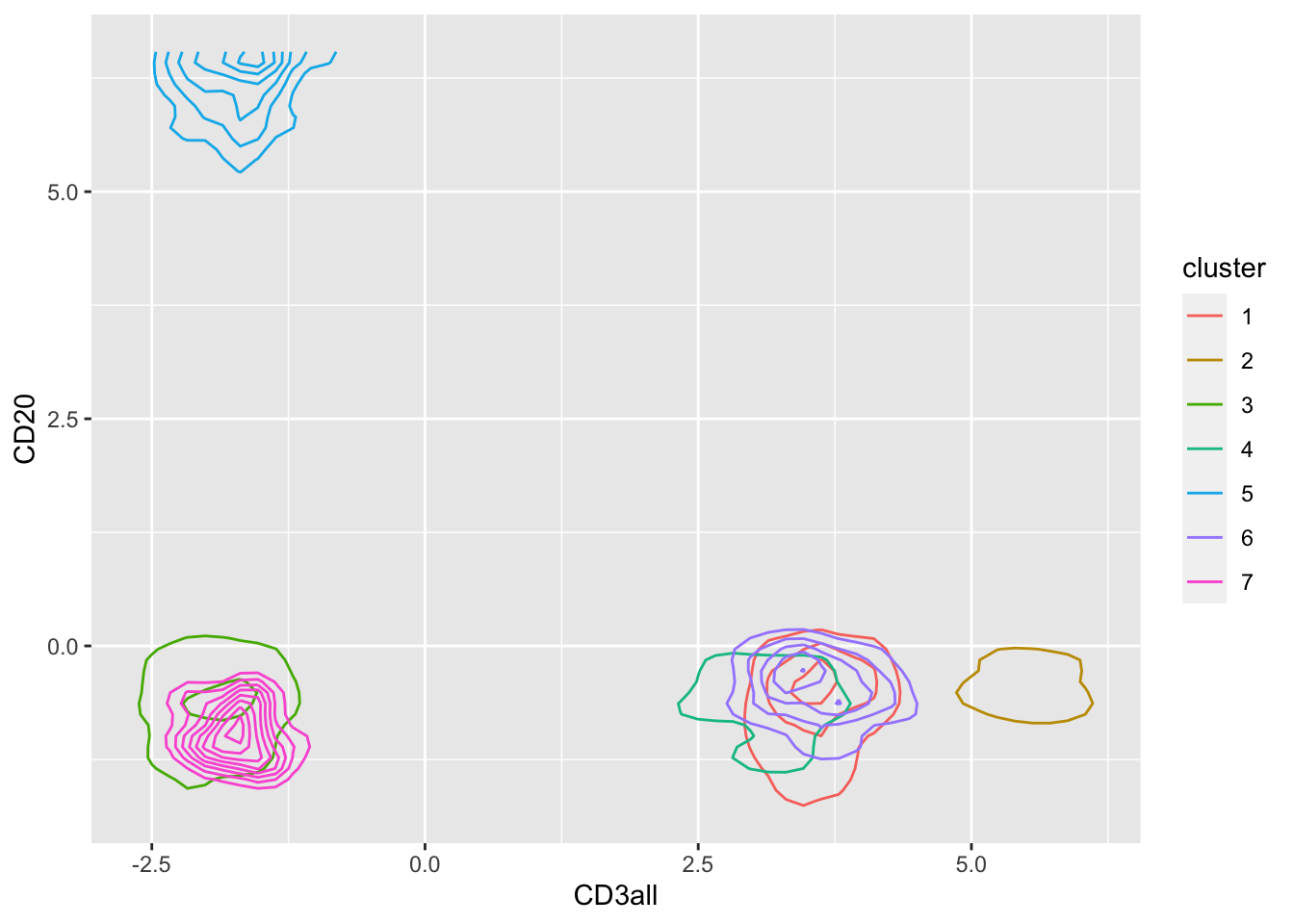
Los dos gráficos muestran el resultado del clustering con dbscan usando 5 marcadores. Se muestran las proyecciones de los datos en CD4-CD8 y C3all-CD20.
7.3 Clustering jerárquico y escogiendo el número de clusters con la estadística gap
Para empezar, simulamos datos provenientes de 4 grupos. Usamos %>% y la función bind_rows del paquete dplyr.
library("dplyr")
simdat = lapply(c(0, 8), function(mx) {
lapply(c(0,8), function(my) {
tibble(x = rnorm(100, mean = mx, sd = 2),
y = rnorm(100, mean = my, sd = 2),
class = paste(mx, my, sep = ":"))
}) %>% bind_rows
}) %>% bind_rows
simdat## # A tibble: 400 x 3
## x y class
## <dbl> <dbl> <chr>
## 1 1.99 -1.53 0:0
## 2 3.00 -2.71 0:0
## 3 2.31 -2.29 0:0
## 4 -2.03 -3.64 0:0
## 5 -3.91 2.64 0:0
## 6 -1.90 1.13 0:0
## 7 2.27 0.125 0:0
## 8 -4.04 0.499 0:0
## 9 -1.02 1.94 0:0
## 10 1.80 3.05 0:0
## # … with 390 more rowssimdatxy = simdat[, c("x", "y")] # without class label
ggplot(simdat, aes(x = x, y = y, col = class)) + geom_point() +
coord_fixed()
Calculamos la suma de cuadrados dentro de los grupos para los grupos obtenidos por el método k-means.
wss = tibble(k = 1:8, value = NA_real_)
wss$value[1] = sum(scale(simdatxy, scale = FALSE)^2)
for (i in 2:nrow(wss)) {
km = kmeans(simdatxy, centers = wss$k[i])
wss$value[i] = sum(km$withinss)
}
ggplot(wss, aes(x = k, y = value)) + geom_col()
El gráfico de barras de la estadística WSS en función de k muestra que el último salto sustancial es justo antes de k = 4. Esto indica que la mejor opción para estos datos es k = 4.
7.3.1 Usando la estadística gap
Vamos a usar el método en un ejemplo real. Primero, cargamos los datos Hiiragi y vemos como se agrupan las células.
## Loading required package: affy## Loading required package: boot##
## Attaching package: 'boot'## The following objects are masked from 'package:gtools':
##
## inv.logit, logit## The following object is masked from 'package:lattice':
##
## melanoma## Loading required package: clue## Loading required package: cluster## Loading required package: geneplotter## Loading required package: annotate## Loading required package: AnnotationDbi##
## Attaching package: 'AnnotationDbi'## The following object is masked from 'package:dplyr':
##
## select## Loading required package: XML## Loading required package: gplots##
## Attaching package: 'gplots'## The following object is masked from 'package:IRanges':
##
## space## The following object is masked from 'package:S4Vectors':
##
## space## The following object is masked from 'package:stats':
##
## lowess## Loading required package: KEGGREST## Loading required package: MASS##
## Attaching package: 'MASS'## The following object is masked from 'package:AnnotationDbi':
##
## select## The following object is masked from 'package:genefilter':
##
## area## The following object is masked from 'package:dplyr':
##
## select## Loading required package: mouse4302.db## Loading required package: org.Mm.eg.db## ## Escogemos los 50 genes más variables.
selFeats = order(rowVars(Biobase::exprs(x)), decreasing = TRUE)[1:50]
embmat = t(Biobase::exprs(x)[selFeats, ])
embgap = clusGap(embmat, FUN = pamfun, K.max = 24, verbose = FALSE)
k1 = maxSE(embgap$Tab[, "gap"], embgap$Tab[, "SE.sim"])
k2 = maxSE(embgap$Tab[, "gap"], embgap$Tab[, "SE.sim"],
method = "Tibs2001SEmax")
c(k1, k2)La opción por default para el número de clusters, k1, es el primer valor de k, para el cual el espacio no es mayor que el primer máximo local menos un error estándar. Esto da una serie de grupos, mientras que la elección recomendada por Tibshirani, Walther y Hastie (2001) es el k más pequeño.
Graficamos la estadística gap.
plot(embgap, main = "")
cl = pamfun(embmat, k = k1)$cluster
table(pData(x)[names(cl), "sampleGroup"], cl)